Запись обозначает число размещений из по элементов. Имеет следующую формулу:
Решим уравнение. Помним, что z должно быть неотрицательным целым числом:
В конце делаем проверку, чтобы нигде не вылезли отрицательные факториалы.
P. S. Я решил эту задачу в уме секунд за 10, потому что помню формулу размещений и тот факт, что , а здесь различается ровно на единицу.
Запись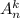 обозначает число размещений из
обозначает число размещений из 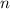 по
по 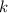 элементов. Имеет следующую формулу:
элементов. Имеет следующую формулу:
Решим уравнение. Помним, что z должно быть неотрицательным целым числом:
В конце делаем проверку, чтобы нигде не вылезли отрицательные факториалы.
P. S. Я решил эту задачу в уме секунд за 10, потому что помню формулу размещений и тот факт, что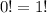 , а здесь
, а здесь 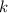 различается ровно на единицу.
различается ровно на единицу.