π/4 + πn, где n ∈ Z;
arctg 1/2 + πk, где k ∈ Z.
Пошаговое объяснение:
cos²x - 3sinxcos x + 2sin²x = 0
Разделим обе части равенства на cos²x , т.к. cos²x ≠ 0.
(Действительно,
если бы cosx = 0, то и sinx = 0, a этого быть не может по основному тригонометрическими тождеству).
Запишем, что
cos²x/cos²x - 3sinxcosx/cos²x + 2sin²x/cos²x = 0
1 - 3tgx + 2tg²x = 0
2tg²x - 3tgx + 1 = 0
Пусть tgx = t, тогда
2t² - 3t + 1 = 0
D = 9 - 8 = 1
t1 = (3+1)/4 = 1;
t2 = (3-1)/4 = 2/4 = 1/2.
Получили, что
tgx = 1 или tgx = 1/2
1) tgx = 1
х = arctg 1 + πn, где n ∈ Z
х = π/4 + πn, где n ∈ Z.
2) tgx = 1/2
х = arctg 1/2 + πk, где k ∈ Z.
Часть 2.
1. Целые числа: -1, 0, 1, 2. Наибольшее: , наименьшее:
2. -0.1
3. х = -0.6
4. 96
5. х = -4.9
Часть 3.
1. x₁ = -1.2 х₂ = -2
2. -5
1. = -0.2, наибольшее число из всех, а = -1 , следовательно наименьшее из них.
2. Я так понимаю это минус в начале выражения? Если да, то:
-7.35+6.5++ = -7.35+6.5+0.25+0.5 = -0.1
3. -1.7+х = -2.3
х = -2.3-(-1.7)
х = -2.3+1.7
х = -0.6
4. -25*(-8)+416:(-4) = 25*8+416:(-4) = 200-104 = 96
5. х = -4.2
х = -4.2 :
х =
х = -4.9
1. |x+1.6| = 0.4
|x+| =
x + 0 x + < 0
x ∞ -∞<x<
(x+) - = 0 (-х-) - = 0
x + = 0 -х-2=0
x₁ = = -1.2 х₂ = -2
2. * 1.47 - * 18.47 = * (1.47-18.47) = * (-17) = -5
π/4 + πn, где n ∈ Z;
arctg 1/2 + πk, где k ∈ Z.
Пошаговое объяснение:
cos²x - 3sinxcos x + 2sin²x = 0
Разделим обе части равенства на cos²x , т.к. cos²x ≠ 0.
(Действительно,
если бы cosx = 0, то и sinx = 0, a этого быть не может по основному тригонометрическими тождеству).
Запишем, что
cos²x/cos²x - 3sinxcosx/cos²x + 2sin²x/cos²x = 0
1 - 3tgx + 2tg²x = 0
2tg²x - 3tgx + 1 = 0
Пусть tgx = t, тогда
2t² - 3t + 1 = 0
D = 9 - 8 = 1
t1 = (3+1)/4 = 1;
t2 = (3-1)/4 = 2/4 = 1/2.
Получили, что
tgx = 1 или tgx = 1/2
1) tgx = 1
х = arctg 1 + πn, где n ∈ Z
х = π/4 + πn, где n ∈ Z.
2) tgx = 1/2
х = arctg 1/2 + πk, где k ∈ Z.
π/4 + πn, где n ∈ Z;
arctg 1/2 + πk, где k ∈ Z.
Часть 2.
1. Целые числа: -1, 0, 1, 2. Наибольшее: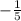 , наименьшее:
, наименьшее: 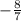
2. -0.1
3. х = -0.6
4. 96
5. х = -4.9
Часть 3.
1. x₁ = -1.2 х₂ = -2
2. -5
Пошаговое объяснение:
Часть 2.
1.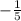 = -0.2, наибольшее число из всех, а
= -0.2, наибольшее число из всех, а 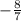 = -1
= -1  , следовательно наименьшее из них.
, следовательно наименьшее из них.
2. Я так понимаю это минус в начале выражения? Если да, то:
-7.35+6.5+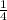 +
+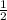 = -7.35+6.5+0.25+0.5 = -0.1
= -7.35+6.5+0.25+0.5 = -0.1
3. -1.7+х = -2.3
х = -2.3-(-1.7)
х = -2.3+1.7
х = -0.6
4. -25*(-8)+416:(-4) = 25*8+416:(-4) = 200-104 = 96
5. х = -4.2
х = -4.2
х = -4.2 :
х =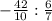
х =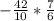
х =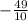
х = -4.9
Часть 3.
1. |x+1.6| = 0.4
|x+ | =
| = 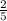
x +
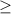 0 x +
0 x +  < 0
< 0
(x+ ) -
) - 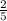 = 0 (-х-
= 0 (-х- ) -
) - 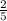 = 0
= 0
x + = 0 -х-2=0
= 0 -х-2=0
x₁ =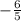 = -1.2 х₂ = -2
= -1.2 х₂ = -2
2.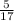 * 1.47 -
* 1.47 - 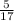 * 18.47 =
* 18.47 = 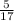 * (1.47-18.47) =
* (1.47-18.47) = 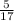 * (-17) = -5
* (-17) = -5