Завдання 8-11 - завдання відкритої форми з розгорнутою відповіддю. висновки, зроблені у розв'язанні, повинні бути достатньо обгрунтованими. 8. коло з центром у точці о(-2; 5) проходить через точку c (1: 1). знайдіть плошу квадрата, вписаного в це коло. 9. бічна сторона рівнобедреного трикутника дорівнює 40 см, а висота, проведена до основи, - 32 см. знайдіть радіус кола, описаного навколо трикутника. 10. периметр і площа прямокутника дорівнюють відповідно 18 см та 20 см. знайти периметр подібного йому прямокутника з площею 5 см. 11. точка 0 - центр описаного кола навколо рівнобедреного прямокутного трикутника 4вс з гіпотенузою b. a(-4; 0), b(0; 4), c(0; 0). знайти координати образа точки о при повороті трикутника навколо вершини сна кут 135° за годинниковою стрілкою.

Пошаговое объяснение:

Из условия можно составить 4 уравнения с четырьмя неизвестными:

A + B = 8

A + C = 13

B + D = 8

C - D = 6

Выразим А и подставим в другие уравнения:

A = 8 - B

8 - B + C = 13     C - B = 5

B + D = 8

C - D = 6

Выразим С и подставим в другие:

C = B + 5

B + D = 8

B + 5 - D = 6     B - D = 1

Сложим два последних уравнения:

B + D = 8

B - D = 1

2B = 9       B = 4,5

В нашли, находим D:

B - D = 1      D = B - 1 = 4,5 -1 = 3,5

Ищем С и А:

C = B + 5 = 4,5 + 5 = 9,5

A = 8 - B = 8 - 4,5 = 3,5

А = 3,5

В = 4,5

С = 9,5

D = 3,5

1. Выполните действия:

а) 

б)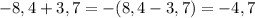 

в) 

г)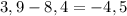 

д) 

е)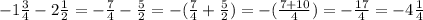 

2. Найдите значение выражения:

1) 

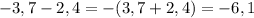
2) 

3) 

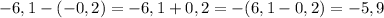
4) 

3. Решите уравнение:

а)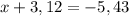 

________________________________________________

(это проверка)

================================================

б) 

4. Найдите расстояние между точками А(-2,8) и В (3,7) на кооординатной прямой.

Исходя из данных условия задания получается прямоугольный треугольник, катеты которого равны 1 и 5 соответственно

по теореме Пифагора: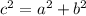 

5. Напишите все целые значения n, если 4 меньше|n|меньше 7.

-6; -5; 5; 6