Вопрос про бесконечность минус бесконечность очень важный. Если Вам дан обычный определенный (собственный) интеграл (интеграл Римана), функция обязана быть ограниченной (хотя этого может и не хватить для существования интеграла). Поэтому ни о какой бесконечности речи быть не может. Если интеграл понимается как несобственный, функция может быть и неограниченной, но если при вычислении предела от первообразной где-то получится бесконечность, интеграл сразу признается расходящимся. Но бывает еще интеграл в смысле главного значения - вот там бесконечности могут скушать друг друга.
Пример. . Как собственный интеграл он не существует (не существует конечный предел интегральных сумм, не зависящий от разбиения и выбора промежуточных точек), как несобственный интеграл он расходится, а в смысле главного значения равен нулю.
Смотрите в объяснениях.
Пошаговое объяснение:
1) 24, 21, 19, 18, 15, 13, __, __, 7.
Разности между членами: 24-21=3, 21-19=2, 19-18=1, 18-15=3, 15-13=2,
13-a=1; a=12, 12-b=3; b=9, 9-2=7.
ответ: 12 и 9.
2) 1, 4, 9, 16, __, __, 49, 64, 81, 100.
Это квадраты чисел от 1 до 10, пропущены 5^2 и 6^2.
ответ: 25 и 36.
3) 16, 17, 15, 18, 14, 19, __, __
Разности между членами: 16-17=-1, 17-15=+2, 15-18=-3, 18-14=+4, 14-19=-5,
19-a=+6, a=19-6=13, 13-b=-7, b=13+7=20.
ответ: 13 и 20.
4) 1, 3, 6, 8, 16, 18, __, __, 76, 78.
1+2=3, 3*2=6, 6+2=8, 8*2=16, 16+2=18, 18*2=36, 36+2=38, 38*2=76, 76+2=78.
ответ: 36 и 38.
5) 7, 26, 19, 5, 21, 16, 9, __, 4.
В каждой тройке второе число равно сумме первого и третьего.
26=7+19, 21=5+16, a=9+4=13.
ответ: 13.
6) 2, 4, 8, 10, 20, 22, __, __, 92, 94.
2+2=4, 4*2=8, 8+2=10, 10*2=20, 20+2=22, 22*2=44, 44+2=46, 46*2=92.
ответ: 44 и 46.
7) 24, 22, 19, 15, __, __.
Разности между членами: 24-2=22, 22-3=19, 19-4=15, 15-5=10, 10-6=4.
ответ: 10 и 4.
Вопрос про бесконечность минус бесконечность очень важный. Если Вам дан обычный определенный (собственный) интеграл (интеграл Римана), функция обязана быть ограниченной (хотя этого может и не хватить для существования интеграла). Поэтому ни о какой бесконечности речи быть не может. Если интеграл понимается как несобственный, функция может быть и неограниченной, но если при вычислении предела от первообразной где-то получится бесконечность, интеграл сразу признается расходящимся. Но бывает еще интеграл в смысле главного значения - вот там бесконечности могут скушать друг друга.
Пример.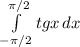
. Как собственный интеграл он не существует (не существует конечный предел интегральных сумм, не зависящий от разбиения и выбора промежуточных точек), как несобственный интеграл он расходится, а в смысле главного значения равен нулю.