А — из случайно отобранных 4 телевизора все хорошие;
В — два хорошие и два нет;
С — один хороший и три нет;
D — хороших нет.
Общее число элементарных исходов равно числу выбрать 4 телевизоров из 16. Т.е.
1) Найдем вероятность события А.
Число благоприятных исходов: выбрать 4 хороших телевизора из 11 можно
Искомая вероятность:
2) Вероятность события В:
Число благоприятных исходов: выбрать два хороших телевизора можно а два НЕ хороших телевизора можно . По правилу произведения, всего таких
3) Вероятность события C:
Выбрать один хороший телевизор можно Выбрать три НЕ хороших телевизора можно По правилу произведения, таких
4) Вероятность события D
Выбрать четыре НЕ хороших телевизора можно
при расчетов:
Будем у каждой сороконожки считать необутые пары ног (значит столько пар им пришлось купить раз ушли все обутые).
1 сороконожка - необута задняя половина из сорока ножек - т.е. необуты 20 ножек - 20 : 2 = 10 пар.
2 сороконожка - необута передняя половина из сорока ножек - т.е. необуты 20 ножек - 20 : 2 = 10 пар.
3 сороконожка - необуты все левые ножки - т.е. необуты 20 ножек - 20 : 2 = 10 пар.
4 сороконожка - необуты все правые ножки - т.е. необуты 20 ножек - 20 : 2 = 10 пар.
Считаем общее количество необутых пар: 10 + 10 + 10 + 10 = 40 пар.
ответ: 40 пар обуви купили сороконожки в магазине.
применяем смекалку.
При внимательном рассмотрении и анализе условия задачи, можно легко заметить, что каждая сороконожка пришла наполовину обутая. Отсюда быстрый подсчет:
4 сороконожки * 40 ножек = 160 ножек
160 ножек : 2 = 80 пар ножек у 4 сороконожек
80 пар : 2 (напополам) = 40 пар необутых ножек
ответ: 40 пар обуви купили сороконожки в магазине.
А — из случайно отобранных 4 телевизора все хорошие;
В — два хорошие и два нет;
С — один хороший и три нет;
D — хороших нет.
Общее число элементарных исходов равно числу выбрать 4 телевизоров из 16. Т.е.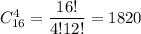
1) Найдем вероятность события А.
Число благоприятных исходов: выбрать 4 хороших телевизора из 11 можно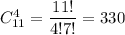
Искомая вероятность:
2) Вероятность события В:
Число благоприятных исходов: выбрать два хороших телевизора можно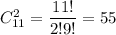 а два НЕ хороших телевизора можно
а два НЕ хороших телевизора можно 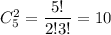 . По правилу произведения, всего таких
. По правилу произведения, всего таких 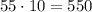
Искомая вероятность:
3) Вероятность события C:
Выбрать один хороший телевизор можно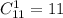 Выбрать три НЕ хороших телевизора можно
Выбрать три НЕ хороших телевизора можно 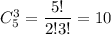 По правилу произведения, таких
По правилу произведения, таких 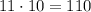
Искомая вероятность:
4) Вероятность события D
Выбрать четыре НЕ хороших телевизора можно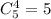
Искомая вероятность: