Запиши формулу, устанавливающую зависимость:
1) числа n купленных тетрадей от их цены a, если стоимость всей покупки равна 600 тенге

Показать ответ

Ответ:

onealoner13

27.08.2020 17:33

ответ: 1). 999; 2).998; 3).996; 4). 997.

Пошаговое объяснение:

Признак делимости на 3: если сумма цифр числа делится на 3, то и само число будет делится на 3;

признак делимости на 2: если число четное, то оно делится на 2.

1). Число "999" делится на 3, так как 9+9+9 делится на 3;

2). число "998" не делится на 3, т.к. сумма его цифр не делится на 3;

3). число "996" делится на 2 и 3, т.к. 9+9+6 делится на 3 и число четное;

4). число "997" не делится ни на 2, ни на 3, т.к. число нечетное и сумма его цифр не делится на 3.

0,0(0 оценок)

Ответ:

напарницавМоскве

17.12.2022 01:16

а) Можно. Для этого удобно брать палочки, идущие подряд. Возьмем первые 5 палочек: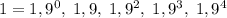 $1=1,9^0,\; 1,9,\; 1,9^2,\; 1,9^3,\; 1,9^4$ .

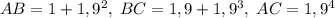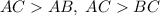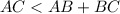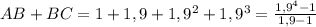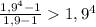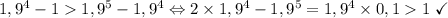Построим треугольник ABC: $AB=1+1,9^2,\; BC=1,9+1,9^3,\; AC=1,9^4$ . Заметим, что $ACAB,\; ACBC$ , поэтому можно не рассматривать неравенства треугольника, включающие эту сторону. Осталось доказать, что . Действительно $AB+BC=1+1,9+1,9^2+1,9^3=\frac{1,9^4-1}{1,9-1}$ по формуле суммы геометрической прогрессии. Но $\frac{1,9^4-1}{1,9-1}1,9^4$ . Проверим истинность этого неравенства: $1,9^{4}-11,9^5-1,9^4 \Leftrightarrow 2\times 1,9^4-1,9^5=1,9^4\times0,11\; \checkmark$ .

б) Предположим, что можно. Тогда, в частности, можно составить два одинаковых отрезка. Рассмотрим набор степеней числа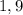 1,9 , которые формируют первый отрезок. Пусть это числа 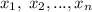$x_{1},\; x_{2},...,x_{n}$ , для второго отрезка возьмем степени 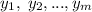$y_{1},\; y_{2},...,y_{m}$ . Получим 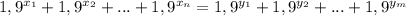$1,9^{x_{1}}+1,9^{x_{2}}+...+1,9^{x_{n}}=1,9^{y_{1}}+1,9^{y_{2}}+...+1,9^{y_{m}}$ (*). Теперь становится ясно, почему это не может быть верно. Ведь то, что мы видим, похоже на запись числа в системе счисления, пусть и "необычной". Но двух различных записей одного числа не бывает. Однако трудно говорить об этом, имея дробную систему счисления. Пусть 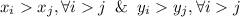$x_{i}x_{j}, \forall ij\;\; \&\;\; y_{i}y_{j},\forall ij$ , другими словами, степени расставлены по порядку. Умножим уравнение на 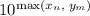$10^{\max(x_{n},\;y_{m})}$ , получим только целые числа вида 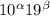$10^{\alpha}19^{\beta}$ . Пусть 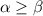$\alpha\geq \beta$ . 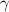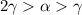Выберем такое число $\gamma$ , что $2\gamma \alpha\gamma$ . Тогда число 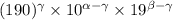$(190)^{\gamma}\times 10^{\alpha-\gamma}\times 19^{\beta-\gamma}$ записано в системе счисления 190, поскольку, как легко видеть, 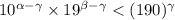$10^{\alpha-\gamma}\times 19^{\beta-\gamma}$ . Отсюда и следует наше противоречие.

Впрочем, кажется, что это перебор, и можно было решить проще: в (*) вычеркнем равные члены с обеих сторон. Получим, что сумма разных степеней равна другой сумме разных степеней. Теперь в левой части к большим степеням перекинем с правой стороны меньшие, а для правой части наоборот. Значит, отрицательное число равно положительному. Противоречие.

Однако для тренировки, мне представляется, было полезно рассмотреть оба подхода.

0,0(0 оценок)

Популярные вопросы: Математика