ответ: Скорость-велосипедиста=300м/минуту,он ехал 15 минут,был и мотоциклист он ехал 800м/м спустя 9 минут мотоциклист догнал велосипедиста
Пошаговое объяснение:
нам понадобиться формула расчёта расстояния
S=v×t S-это расстояние V-это с какой скоростью едет, ну допустим мотоциклист .его V=800 T-это какое время объект ехал или шёл у велосипедиста это 15 минут. давайте решать!
узнаем сколько проехал велосипедист
S=300×15=4500(м)
Теперь узнаём методом подбора...и так я посчитал и подобрал число и это 9 и так проверяем
S=800×9=7200(м) вот мы узнали сколько проехал мотоциклист
Вы помните мы узнали сколько проехал велосипедист?Это нам сейчас пригодиться
S=300×9=2700(м)
(м)-метры
складываем 4500+2700=7200(м)
Вот! мотоциклист догнал велосипедиста и мы решили задачу
Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:
Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.
Тогда большее число в -той паре будет равно , а их (бОльших чисел) последовательность выглядеть так:
Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму первых 2020 элементов арифметической прогрессии с первым элементом и разностью :
С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:
Сумму чисел во вторых скобках опять же найдем как сумму первых 1010 элементов арифметической прогрессии с первым элементом и разностью :
Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:
Отсюда
Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.
ответ: Скорость-велосипедиста=300м/минуту,он ехал 15 минут,был и мотоциклист он ехал 800м/м спустя 9 минут мотоциклист догнал велосипедиста
Пошаговое объяснение:
нам понадобиться формула расчёта расстояния
S=v×t S-это расстояние V-это с какой скоростью едет, ну допустим мотоциклист .его V=800 T-это какое время объект ехал или шёл у велосипедиста это 15 минут. давайте решать!
узнаем сколько проехал велосипедист
S=300×15=4500(м)
Теперь узнаём методом подбора...и так я посчитал и подобрал число и это 9 и так проверяем
S=800×9=7200(м) вот мы узнали сколько проехал мотоциклист
Вы помните мы узнали сколько проехал велосипедист?Это нам сейчас пригодиться
S=300×9=2700(м)
(м)-метры
складываем 4500+2700=7200(м)
Вот! мотоциклист догнал велосипедиста и мы решили задачу
нет
Пошаговое объяснение:
Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:
Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.
Тогда большее число в -той паре будет равно
-той паре будет равно 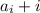 , а их (бОльших чисел) последовательность выглядеть так:
, а их (бОльших чисел) последовательность выглядеть так:
Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму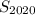 первых 2020 элементов арифметической прогрессии с первым элементом
первых 2020 элементов арифметической прогрессии с первым элементом 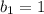 и разностью
и разностью 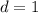 :
:
С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:
Сумму чисел во вторых скобках опять же найдем как сумму первых 1010 элементов арифметической прогрессии с первым элементом
первых 1010 элементов арифметической прогрессии с первым элементом 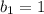 и разностью
и разностью 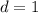 :
:
Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:
Отсюда
Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.