За 4 дні 2 кравчині шиють 16 комплектів постільної білизни. За скільки днів одна кравчині пошиє 10 комплектів

Показать ответ

Ответ:

456akcyka

08.10.2021 18:02

506√3 см²

Пошаговое объяснение:

Один из углов равнобедренной трапеции равен 150°. Вычисли площадь трапеции, если её меньшее основание равно 13 см, а боковая сторона равна 22√3 см.

Дано: АВСД - трапеция, АВ=СД=22√3 см.

ВС=13 см.

Найти S.

Решение: Проведем две высоты ВН и СК. Рассмотрим Δ АВН - прямоугольный.

∠АВН=150-90=60°, тогда ∠А=30°, а ВН=12 АВ=11√3 см. (как катет, лежащий против угла 30°)

Найдем АН по теореме Пифагора:

АН²=(22√3)² - (11√3)² = 1452-363=1089; АН=√1089=33 см.

ДК=АН=33 см

АД=АН+КН+ДК=33+13+33=79 см.

S=(13+79):2*11√3=506√3 cм²

ответ: 506√3 см²

0,0(0 оценок)

Ответ:

ilyusha462782

17.12.2020 14:05

Оценим максимальное значение, которое может принимать элемент множества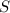 . Предположим, что существуют хотя бы два элемента множества, больших 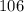106 . Пусть это числа 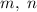$m,\;n$ . Положим 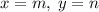$x=m,\; y=n$ , тогда 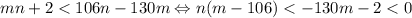mn+2 , откуда 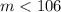. Противоречие. Значит, существует не более одного числа, большего

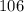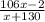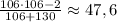Теперь становится ясно, как строить множество. Пусть максимальное число равно 106 . Тогда следующее по величине число меньше $\frac{106x-2}{x+130}$ , где — текущее число (сейчас рассматривается максимальное число; оценка следует из исходного уравнения). То есть второе по величине число не превосходит $\frac{106\cdot 106-2}{106+130}\approx 47,6$ . Берем 47. Далее: 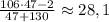$\frac{106\cdot 47-2}{47+130}\approx 28,1$ . Берем 28. И так далее. Получим множество 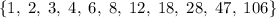$\{1,\;2,\;3,\;4,\;6,\;8,\;12,\;18,\;28,\;47,\;106\}$ , состоящее из 11 элементов. Это и есть наш ответ.