Яблоневый сад имеет длину 140м,ширину 72м.сколько в саду высажено яблань,если на каждую яблоню в среднем приходиться 12м?

Показать ответ

Ответ:

Саня200763

14.01.2022 19:21

Пошаговое объяснение:

1)3х - 5 = 16

3х= 16+5

3х=21

х= 21:3

х=7

7+р= 15

р= 15-7

р= 8

2) х/8+ ( х-1)/4=5

х+2(х-1)=5*8

х+2х-2=40

3х= 40+2

3х=42

х=42:3

х= 14

3)4|х-5|=36

4(х-5)=36

4х-20= 36

4х= 56

х= 56 :4

х₁=14

4(х-5)=-36

4х-20=- 36

4х= -16

х= -16 :4

х₂= -4

4) Пусть во втором букете- х лилий, тогда в первом букете - 3х лилий, когда к первому букету добавили 2 лилии в нем стало 3х+2, а

ко второму 8 лилий, то в нем стало х+8 лилий. Составим уравнение:

3х+2= х+8

3х-х= 8-2

2х= 6

х= 6:2

х= 3 лилии во втором букете первоначально

3х= 3*3= 9 лилий в первом букете первоначально

0,0(0 оценок)

Ответ:

КкапризЗ

12.03.2023 19:01

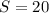Δ АВС- равнобедренный, S=20 кв. ед.

Пошаговое объяснение:

Найдем стороны треугольника, воспользовавшись формулой расстояния между точками

$d= \sqrt{(x{_1}- x{_2})^{2}+(y{_1}-y{_2})^{2} }$

$A(-4;-2); B(-2;4) \\AB=\sqrt{(-4+2) ^{2}+(-2-4) ^{2} } =\sqrt{(-2)^{2} +(-6)^{2} } =\sqrt{4+36} =\sqrt{40}=2\sqrt{10} ;$

$A(-4;-2); C(4;2)\\AC= \sqrt{(-4-4) ^{2} +(-2-2)^{2} } =\sqrt{(-8)^{2} +(-4)^{2} } =\sqrt{64+16} =\sqrt{80} =4\sqrt{5} ;$

$B(-2;4); C( 4;2) \\BC= \sqrt{(-2-4)^{2} +(4-2) ^{2} } =\sqrt{(-6)^{2} +2^{2} } =\sqrt{36+4} =\sqrt{40} =2\sqrt{10} .$

Так как AB=BC , то Δ АВС - равнобедренный.

Проведем высоту ВМ, в равнобедренном треугольнике она является и медианой.

Значит, АМ= МС= 4√5: 2=2√5 ед.

Рассмотрим прямоугольный треугольник Δ АМВ и найдем катет ВМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.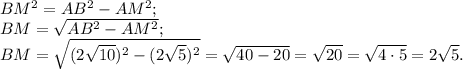 $BM^{2} =AB^{2} -AM^{2} ;\\BM = \sqrt{AB^{2} -AM^{2} } ;\\BM= \sqrt{(2\sqrt{10})^{2} - (2\sqrt{5})^{2} } =\sqrt{40-20} =\sqrt{20} =\sqrt{4\cdot5} =2\sqrt{5} .$