Y=x2, y=2x+5, y=11, y=x3, y=x, y=-3x-8, y=-0,5x+1, y=-12, y=-x, y=x2 +16, y=4x-3, y=7x А)Выпишите линейные функции, укажите после запятой коэффициент.

Б)- Сколько точек достаточно для построения графиков этих функций?

В)- Как могут располагаться две произвольные прямые на плоскости?

Перед вами графики линейных функций с алгеброй уже через 15 минут сдавать

Y=x2, y=2x+5, y=11, y=x3, y=x, y=-3x-8, y=-0,5x+1, y=-12, y=-x, y=x2 +16, y=4x-3, y=7x А)Выпишите ли

Показать ответ

Ответ:

renger100

21.07.2022 23:02

4826390517

Пошаговое объяснение:

Числа 5 и 7 могут стоять только рядом с 0 или 1.

Поскольку 0 и 1 можно использовать только по одному разу, значит ответ должен либо начинаться одной из последовательностей:

7150*, 5170*, 7051*, 5071*

либо заканчиваться на:

*0517, *0715, *1507, *1705

Выберем только наименьшие из этих последовательностей. Остаётся два варианта: либо число начинается с 5071, либо заканчивается на 0517. Так, имеем два возможных варианта:

5071

0517

Число 9 может стоять рядом с 0, 1 и 3. Поскольку 0 и 1 мы уже использовали выше, значит 9 должна быть быть рядом:

50719

90517

Следующей цифрой может быть только 3:

507193

390517

Далее только 6:

5071936xxx

xxx6390517

За ней только 2:

50719362xx

xx26390517

У нас осталось две цифры: 4 и 8. Обе могут быть добавлены к результирующему числу в любом порядке. Очевидно, что 84 больше, чем 48, поэтому не будем рассматривать такой вариант. Прибавим 48:

5071936248

4826390517

Итого, мы получили 2 числа, удовлетворяющих условию задачи. Выберем среди них наименьшее. Это будет число 4826390517, что и является ответом к задаче.

0,0(0 оценок)

Ответ:

Кооооотттт

07.02.2020 08:11

$C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

или

$2\,\,753\,\,294\,\,408\,\,504\,\,640$

Пошаговое объяснение:

Давайте сначала введём понятие.

Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать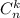 C^k_n и определим формулой

$\displaystyle C^k_n=\frac{n!}{k!(n-k)!}$

Если нужно доказательство, пишите

Итак, приступаем к решению.

Сначала раздаем первому игроку.

Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.

$\displaystyle C^{10}_{32}=\frac{32!}{10!(32-10)!}= \frac{22!*23*24*25*26*27*...*32}{22!*10*9*8*7*6*5*4*3*2} =\\=\frac{23*24*25*26*37*...*35}{10*9*8*7*6*5*4*3*2}=64512240$

Но можно было просто оставить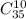 $C^{10}_{35}$

Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.

Тогда количество раздать второму 10 карт из 22 - это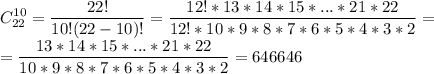 $\displaystyle C^{10}_{22}=\frac{22!}{10!(22-10)!}=\frac{12!*13*14*15*...*21*22}{12!*10*9*8*7*6*5*4*3*2}=\\=\frac{13*14*15*...*21*22}{10*9*8*7*6*5*4*3*2}=646646$

Или опять же можно было бы оставить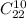 $C^{10}_{22}$

Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно

$\displaystyle C^{10}_{12}=\frac{12!}{10!(12-10)!}=\frac{12*11*10!}{10!*2}=66$

Ну хоть здесь нормальное число. Но опять же можно было и оставить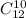 $C^{10}_{12}$

И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.

Получим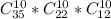 $C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

Или если в числах, то это

$64512240*646646*66=2753294408504640=2\,\,753\,\,294\,\,408\,\,504\,\,640$