К бассейну проведены три трубы. Если по первой и второй трубе вода в бассейн поступает, то через третью трубу вода сливается. Первая труба наполняет бассейн за 6 часов, вторая – за 8 часов. Через третью трубу вода из бассейна вытекает через за 4 часа. За какое время наполнится 3/4 части бассейна, если включить все три трубы?
1 - объём воды в бассейне;
1) 1 : 6 = 1/6 - часть бассейна наполняет первая труба за час;
2) 1 : 8 = 1/8 - часть бассейна наполняет вторая труба за час;
3) 1 : 4 = 1/4 - часть бассейна сливает третья труба за час;
4) 1/6 + 1/8 - 1/4 = 4/24 + 3/24 - 6/24 = 1/24 - часть бассейна наполнится за час;
5) 3/4 : 1/24 = (3 * 24)/4 = 18 (часов) - за это время наполнится 3/4 части бассейна, если включить все три трубы.
В решении.
Пошаговое объяснение:
К бассейну проведены три трубы. Если по первой и второй трубе вода в бассейн поступает, то через третью трубу вода сливается. Первая труба наполняет бассейн за 6 часов, вторая – за 8 часов. Через третью трубу вода из бассейна вытекает через за 4 часа. За какое время наполнится 3/4 части бассейна, если включить все три трубы?
1 - объём воды в бассейне;
1) 1 : 6 = 1/6 - часть бассейна наполняет первая труба за час;
2) 1 : 8 = 1/8 - часть бассейна наполняет вторая труба за час;
3) 1 : 4 = 1/4 - часть бассейна сливает третья труба за час;
4) 1/6 + 1/8 - 1/4 = 4/24 + 3/24 - 6/24 = 1/24 - часть бассейна наполнится за час;
5) 3/4 : 1/24 = (3 * 24)/4 = 18 (часов) - за это время наполнится 3/4 части бассейна, если включить все три трубы.
Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
Пошаговое объяснение:
Требуется найти, через какое время моторная лодка встретится с плотом после выхода из пункта B.
Плот проплывает расстояние между пунктами A и B за 20 часов. Такое же расстояние моторная лодка проплывает по озеру за 5 часов.
Вспомним формулы:
1. Пусть расстояние от А до В - S км.
Тогда скорость плота - Vтеч. =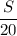 км/ч.
км/ч.
Заметим, что скорость плота равна скорости течения.
Собственная скорость лодки - Vл =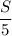 км/ч.
км/ч.
⇒
Скорость лодки по течению:
Vпо теч. = Vл+Vтеч. =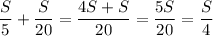 (км/ч)
(км/ч)
Скорость лодки против течения:
Vпр.теч. = Vл - Vтеч. =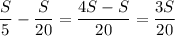 (км/ч)
(км/ч)
2. Рассмотрим движения из пункта А в пункт В.
Скорость плота -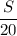 км/ч; скорость лодки по течению -
км/ч; скорость лодки по течению - 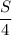 км/ч
км/ч
⇒ скорость лодки по течению в 5 раз больше, чем скорость плота.
То есть, когда лодка приплывет в пункт В, плот проплывет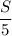 км и будет находиться в М.
км и будет находиться в М.
3. Когда плот оказался в точке М, лодка развернулась и поплыла против течения со скоростью -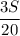 км/ч.
км/ч.
Теперь можем считать, что одновременно навстречу друг другу выплыли плот и лодка соответственно из М и В, расстояние между которыми
Найдем искомое время до их встречи.
Для этого найдем скорость сближения:
Vc = Vп + Vпр.теч. =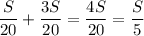 (км/ч)
(км/ч)
4. Зная расстояние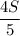 км и скорость
км и скорость 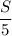 км/ч, мы можем найти искомое время:
км/ч, мы можем найти искомое время:
Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.