Выполни 1)Выполнить следующее задание:

Проведите прямые через каждые две точки. Сколько общих точек имеет каждая из прямых с окружностью.

ответ.

Прямая и окружность не имеют общих точек.

Прямая и окружность имеют только одну точку.

Прямые , , , и окружность имеют две общие точки.

2) Определить взаимное расположении прямой и окружности, если:

1. R=16cм, d=12см

2. R=5см, d=4,2см

3. R=7,2дм, d=3,7дм

4. R=8 см, d=1,2дм

5. R=5 см, d=50мм

а) прямая и окружность не имеют общих точек;

б) прямая является касательной к окружности;

в) прямая пересекает окружность.

d-расстояние от центра окружности до прямой, R- радиус окружности.​

17.

1-2y=3

-2y = 3 - 1

-2y = 2 | : (-2)

y = -1

x = 1 - (-1) = 1+1 = 2

ответ: (2;-1)

18.

2 sin²x + 5 cos x + 1 = 0

Из основного тригонометрического тождества sin²x + cos²x = 1 выразим sin²x

sin²x  = 1-cos²x

2 * (1-cos²x) + 5 cos x + 1 = 0

2-2cos²x + 5 cos x + 1 = 0 | :(-1)

2cos²x - 5 cos x - 3 = 0

Пусть  cos x=t, тогда

2t² - 5t - 3 = 0

D = (-5)² - 4*2*(-3) = 25 + 24 = 29 = 7²

Вернёмся к замене:

Т.к. в уравнении cos x = a есть условие, что |a|≤1, то используем только второй корень

, n∈Z

, n∈Z

,n∈Z

,n∈Z

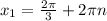ответ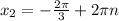: ,n∈Z ; ,n∈Z

Пошаговое объяснение:

нам надо найти наименьшее  число, которое делится одновременно на все дни круизов. на 12, на 18 и на 24

это число называется наименьшее общее кратное.

чтобы найти НОК надо  разложить числа на простые множители.  

24 = 2 * 2 * 2 * 3

12 = 2 * 2 * 3

18 = 2 * 3 * 3

теперь берем и  выписываем все множители бОльшего числа и добавляем к ним из других чисел те множители, которых не хватает.

из 12 брать нечего, т.к. 24 и так кратно 12, а вот из 18 возьмем недостающую тройку и получим

НОК (12; 18; 24) = 2 · 2 · 2 · 3 · 3 = 72

подчеркнутые множители - это из 24, а еще одна тройка из 18

вот. встретятся все вместе в порту через 72 дня