Вычислите:
Р4 24
120
132
630

Показать ответ

Ответ:

hihilaim

08.11.2022 11:13

1 (-бесконечность;+бесконечность) 2 (- бесконечность;-7\4)U(-7\4;+бесконечность) 3 [-7;+бесконечность) 4 (-бесконечность;1/2) 5(-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность) 6(-бесконечность;+бесконечность)

Пошаговое объяснение:

Область определения это такие числа, которые может принимать переменная x.

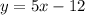1. y=5x-12 (здесь при любых числах выражение решается,т.е. нет ограничений => (-бесконечность;+бесконечность)

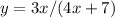2. y=3x/(4x+7) (В данном случае, ограничение присутствует, знаменатель дроби не должен быть равен нулю. (старое правило-на 0 делить нельзя)

$4x+7 \neq 0$

$x \neq -7/4$ => (- бесконечность;-7\4)U(-7\4;+бесконечность)

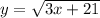3. $y=\sqrt{3x+21}$ (Под корнем всегда должно быть неотрицательное число)

$3x+21\geq 0\\x\geq -7$ [-7;+бесконечность)

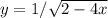4. $y=1/\sqrt{2-4x}$ (знаменатель не должен быть равен 0, а так же не должен быть отрицательным)

$2-4x0\\x$ (-бесконечность;1/2)

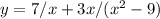5. $y=7/x+3x/(x^{2} -9)$ (знаменатель не должен быть равен 0)

$x\neq 0 и x^{2} -9\neq 0\\x\neq 0 и (x-3)(x+3)\neq 0\\x\neq 0 и x\neq +-3$ (-бесконечность;3)U(-3;0)U(0;3)U(3;+бесконечность)

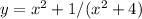6. $y=x^{2} +1/(x^{2} +4)\\\\$ (знаменатель не должен быть равен 0, но если решить, можно понять что знаменатель положителен при любых x)

(-бесконечность;+бесконечность)

0,0(0 оценок)

Ответ:

driftstiwrx

12.04.2022 05:51

24·x²–34·x+25·y²=39

Пошаговое объяснение:

Пусть (x; y) координаты точки M, то есть M(x; y), d₁ – расстояние от точки M(x; y) до точки А(1; 0), а d₂ – расстояние от точки M(x; y) до прямой x=8.

Проекцией точки M(x; y) на ось Ох будет точкой В(x; 0) (см. рис). Тогда расстояние d₁ можем найти из прямоугольника треугольника AMB с катетами

АВ = (х–1) и ВM = у.

Применим теорему Пифагора: d₁²=(х–1)²+у².

Далее, расстояние от точки M(x; y) до прямой x=8 равно

d₂=|8–х|.

По условию задачи

5·d₁ = d₂ или 25·d₁² = d₂².

Получим уравнение:

25·((х–1)²+у²) = (8–х)².

Упростим уравнение:

25·x²–50·x+25+25·y²–x²+16·x=64

24·x²–34·x+25·y²=39.