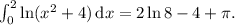Пошаговое объяснение:
Для вычисления интеграла воспользуемся сначала методом интегрирования по частям:
Заметим, что , и тогда в интеграле после интегрирования по частям напрашивается такая замена:
Если , то, положив , найдём, что:
Применим это всё при вычислении получившегося интеграла.
Пределы интегрирования изменятся так:
Вычислим теперь сам интеграл:
Введём замену:
Продолжим вычисление интеграла:
Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:
Наконец, получаем, что
Пошаговое объяснение:
Для вычисления интеграла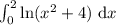 воспользуемся сначала методом интегрирования по частям:
воспользуемся сначала методом интегрирования по частям:
Заметим, что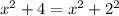 , и тогда в интеграле после интегрирования по частям напрашивается такая замена:
, и тогда в интеграле после интегрирования по частям напрашивается такая замена:
Если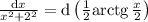 , то, положив
, то, положив 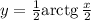 , найдём, что:
, найдём, что:
Применим это всё при вычислении получившегося интеграла.
Пределы интегрирования изменятся так:
Вычислим теперь сам интеграл:
Введём замену: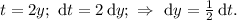
Пределы интегрирования изменятся так:
Продолжим вычисление интеграла:
Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:
Наконец, получаем, что