Рисунок простой, поэтому прямоугольный параллелепипед ABCDA1B1C1D1 с отрезками AC и AB1 построишь самостоятельно.
Решение. Угол В1АВ - линейный угол двугранного угла B1ADB (ВА перпендикулярно АD т к по условию ABCDA1B1C1D1 - прямоугольный параллелепипед, В1А перпендикулярно АD по теореме о трех перпендикулярах). Т к ABCD - квадрат и АС=6√2, то АВ=6.
Обозначим всю работу за единицу, тогда первый маляр работает со скоростью (производительностью) , а второй - .
Значит работая вместе, они работают со скоростью
Время, которое потребуется на выполнение работы со скоростью находим как работу деленную на скорость ее выполнения:
(ч.)
P.S. Обозначение объема работы или всей работы за единицу - стандартный прием при решении таких задач, когда нет количественного выражения работы, т.е. явно не сказано в каком объеме или количестве что-либо сделали.
Рисунок простой, поэтому прямоугольный параллелепипед ABCDA1B1C1D1 с отрезками AC и AB1 построишь самостоятельно.
Решение. Угол В1АВ - линейный угол двугранного угла B1ADB (ВА перпендикулярно АD т к по условию ABCDA1B1C1D1 - прямоугольный параллелепипед, В1А перпендикулярно АD по теореме о трех перпендикулярах). Т к ABCD - квадрат и АС=6√2, то АВ=6.
cos\angle B_1AB= \frac{AB}{AB_1}= \frac{6}{4 \sqrt{3}}= \frac{ \sqrt{3}}{2};cos∠B1AB=AB1AB=436=23;
\angle B_1AB=30к.∠B1AB=30к.
Двугранный угол B1ADB = 30°
32 часа
Пошаговое объяснение:
Обозначим всю работу за единицу, тогда первый маляр работает со скоростью (производительностью)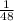 , а второй -
, а второй - 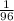 .
.
Значит работая вместе, они работают со скоростью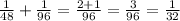
Время, которое потребуется на выполнение работы со скоростью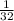 находим как работу деленную на скорость ее выполнения:
находим как работу деленную на скорость ее выполнения:
P.S. Обозначение объема работы или всей работы за единицу - стандартный прием при решении таких задач, когда нет количественного выражения работы, т.е. явно не сказано в каком объеме или количестве что-либо сделали.