Вурне лежит 11 шаров, из которых 5 белых и 6 черных. в эту урну добавили еще 1 шар неизвестного цвета, но известно, что добавленный шар с вероятностью 0,35 - белый, а с вероятностью 0,65 - черный. после этого из урны стали по одному выбирать шары. какова вероятность того, что первый выбранный шар - белый. какова вероятность того, что добавленный шар белый, если известно, что первый выбранный шар - белый. какова вероятность того, что первый выбранный шар одинакового цвета с добавленным. что-то из этого уже решил, хочу проверить и узнать каким вы считали.
32 : 2 = 16 16 : 2 = 8
16 : 2 = 8 8 : 2 = 4
8 : 2 = 4 4 : 2 = 2
4 : 2 = 2 2 : 2 = 1
2 : 2 = 1 32 = 2 * 2 * 2 * 2 * 2
64 = 2 * 2 * 2 * 2 * 2 * 2
НОК (64 и 32) = 2 * 2 * 2 * 2 * 2 * 2 = 64 - наименьшее общее кратное
64 : 64 = 1 64 : 32 = 2
НОД (64 и 32) = 2 * 2 * 2 * 2 * 2 = 32 - наибольший общий делитель
64 : 32 = 2 32 : 32 = 1
Пошаговое объяснение:
1) Сначала определим количество выборов стульев для гостей.
Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).
Число сочетаний из n элементов по k обозначается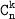
и равно:
где m!=1·2·3·...·(m-1)·m.
Тогда, по условию задачи общее количество стульев n=8 и нужно выбрать стульев k=4:
2) Теперь определим количество рассадки 4-х гостей на 4-х стульях. Так как каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
P₄=4!.
3) Количество необходимых для рассадки 4-х гостей на 8-ми стульях определим как произведения число сочетаний на перестановку: