Вмагазине листы фанеры одинаковой толщины. у кого производителя цена за 1 квадратный метр наименьшая? "хвойный мир" 1400мм 1600мм 252р оао "фанера-xxi век" 1500мм 1800мм 297р пао "леший" 1900мм 2000мм 437р ! впр

Дано:

1 клетка - 1 см²

Длина клетки - 1 см

Длина первого прямоугольника (a¹) - ? см

Ширина первого прямоугольника (b¹) - ? см

Длина второго прямоугольника (a²) - ? см

Ширина второго прямоугольника (b²) - ? см

Найти:

Площадь первого прямоугольника (S¹) - ?

Площадь второго прямоугольника (S²) - ?

(Площадь прямоугольника равняется количеству квадратных мм, см, дм, м, км и т.д)

S = a × b (S = ab)

1) a¹ = 4 см

b¹ = 9 см

S¹ = a¹ × b¹ (S¹ = a¹b¹)

S¹ = 4 × 9 = 36 см²

2) a² = 4 см

b² = 7 см

S² = a² × b² (S² = a²b²

S² = 4 × 7 = 28 см²

ответ: S¹ = 36 см²; S² = 28 см².

Удачи Вам! :)

В основной квадрат (со стороной 32см) вписывается бесконечное количество последующих квадратов, сторона которых равна половине диагонали предыдущего.

Площадь первого равна 32*32 = 1024

Площадь второго равна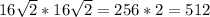

Замечаем, что это убывающая геометрическая прогрессия , знаменатель которой равен 1/2

Сумму площадей всех последующих квадратов можно посчитать по формуле суммы бесконечно убывающей геом. прогрессии

сторона третьего квадрата равна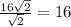 единиц

Наибольший квадрат - первый, и его площадь равна 32*32 = 1024 кв.ед

Знаменатель геом. прогрессии равен 1/2 или 0,5