Виюле 2016 года планируется взять кредит в банке - вопрос №20166235460 от deniskim01 20.09.2022 18:30

Question

Математика: Виюле 2016 года планируется взять кредит в банке в размере s тыс. рублей, где s — натуральное число, на 3 года. условия его возврата таковы − каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года; − с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; − в июле каждого года долг должен составлять часть кредита в соответствии со следующим графиком: июль 2016 - s ; июль 2017 - 0,7s ; июль 2018 - 0,4s ; июль 2019 - 0 рублей. найдите наименьшее значение

deniskim01 · Answer

Если долг увеличивается на 15%, то это тоже самое, что увеличить в 1,15 раз.

Запишем какая была задолженность в январе и июле с 2016 по 2019 годы.

07.2016: S

01.2017: 1,15S

07.2017: 0,7S

01.2018: 1,15·0,7S = 0,805S

07.2018: 0,4S

01.2019: 1,5·0,4S = 0,46S

07.2019: 0

С 2017 по 2019 годы, раз в год выплачивали часть долга (с февраля по июнь). Определим взносы на основе вышеизложенных данных.

2017: 1,15S-0,7S = 0,45S

2018: 0,805S-0,4S = 0,405S

2019: 0,46S-0 = 0,46S

Все выплаты были целыми, поэтому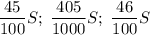 $\dfrac{45}{100}S;\; \dfrac{405}{1000}S;\; \dfrac{46}{100}S$ - целые числа.

$\dfrac{45}{100}S =\dfrac{9}{20}S$

$\dfrac{405}{1000}S =\dfrac{81}{200}S$

$\dfrac{46}{100}S =\dfrac{23}{50}S$

Наименьшему S соответствует НОК(20;200;50).

200⋮20 и 200⋮50 ⇒ НОК(20;200;50)=200

S=200

ответ: 200.