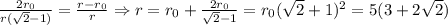Величина кута АВC дорівнює 140°. Промінь BDлежить між сторонами кута АВC. Знайдіть величину ∠ABD (у градусах), якщо ∠ABD : ∠DBC= 2 : 5.

Показать ответ

Ответ:

mariabilyk2005

11.02.2020 17:00

AB=x – по условию;

Сказано, что СВ на 3 сантиметра меньше стороны АВ, значит сторона СВ=х-3;

Сторона СD в 1,125 раз больше стороны АВ, значит сторона СD=1,125*x;

Сторона AD в 3 раза больше стороны СD, значит сторона AD= 1,125x+3;

По условию сказано, что периметр четырехугольника равен 10,2 сантиметров. Периметр - это сумма длин всех сторон фигуры. Составляем уравнение:

х+(х-3)+1,125х+(1,125х+3)=10,2;

4,25x=10,2;

x= 10,2/4,25;

x=2,4.

ответ: х=2,4 см.

Условие некорректно, так как сторона СВ=2,4-3=-0,6 - отрицательное число, чего не может быть!

Пошаговое объяснение:

0,0(0 оценок)

Ответ:

zukhra9087

22.05.2021 14:24

Заметим, что множество точек, являющихся центрами окружностей, вписанных в угол, лежит на биссектрисе этого угла. Касание двух окружностей может быть внутренним, а может быть внешним. Случай внутреннего касания, очевидно, невозможен. Остается лишь случай внешнего (единственность).

Рассмотрим бесконечную серию окружностей вписанных в этот угол. Понятно, что радиусы окружностей убывают как геометрическая прогрессия (здесь наблюдается преобразование подобия — гомотетия). Пусть радиус меньшей окружности (с радиусом 5) равен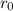 $r_{0}$ . Тогда отрезок, начало которого в вершине прямого угла, а конец в центре большой окружности, можно посчитать через сумму бесконечной геометрической прогрессии: 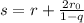$s=r+\frac{2r_{0}}{1-q}$ , где 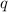— отношение радиусов соседних окружностей. С другой стороны, по теореме Пифагора: 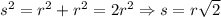$s^2=r^2+r^2=2r^2 \Rightarrow s=r\sqrt{2}$ . Имеем: 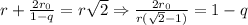$r+\frac{2r_{0}}{1-q}=r\sqrt{2} \Rightarrow \frac{2r_{0}}{r(\sqrt{2}-1)}=1-q$ , причем 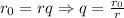$r_{0}=rq \Rightarrow q=\frac{r_{0}}{r}$ , откуда $\frac{2r_{0}}{r(\sqrt{2}-1)}=\frac{r-r_{0}}{r} \Rightarrow r=r_{0}+ \frac{2r_{0}}{\sqrt{2}-1}=r_{0}(\sqrt{2}+1)^2=5(3+2\sqrt{2})$