Многоуго́льник — это геометрическая фигура, обычно определяется как замкнутая ломаная.
Существуют три различных варианта определения многоугольника:
Плоская замкнутая ломаная; Плоская замкнутая ломаная без самопересечений; Часть плоскости, ограниченная замкнутой ломаной.
В любом случае, вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с чётырьмя — четырёхугольником, с пятью — пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.
Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади.
Многоугольник называют выпуклым, если выполнено одно из следующих (эквивалентных) условий: он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (то есть продолжения сторон многоугольника не пересекают других его сторон) ; он является пересечением (то есть общей частью) нескольких полуплоскостей; Каждая диагональ лежит внутри многоугольника; любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит.
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны, например равносторонний треугольник, квадрат и правильный пятиугольник. Правильный многоугольник с самопересечениями называется звёздчатым, например, правильные пятиконечная и восьмиконечная звёзды.
Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°.
Существуют три различных варианта определения многоугольника:
Плоская замкнутая ломаная;
Плоская замкнутая ломаная без самопересечений;
Часть плоскости, ограниченная замкнутой ломаной.
В любом случае, вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с чётырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
Многоугольник с n вершинами называется n-угольником.
Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади.
Многоугольник называют выпуклым, если выполнено одно из следующих (эквивалентных) условий:
он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (то есть продолжения сторон многоугольника не пересекают других его сторон) ;
он является пересечением (то есть общей частью) нескольких полуплоскостей;
Каждая диагональ лежит внутри многоугольника;
любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит.
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны, например равносторонний треугольник, квадрат и правильный пятиугольник.
Правильный многоугольник с самопересечениями называется звёздчатым, например, правильные пятиконечная и восьмиконечная звёзды.
Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом, он может принимать значения от -180° до 180°.
Необходимо сложить первые 16 последовательных натуральных чисел
Пошаговое объяснение:
Данная последовательность представляет арифметическую прогрессию, первый член которой равен 1, последний a(n) и разность прогрессии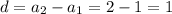
Сумма данной арифметической прогрессии
По условию, сумма данной прогрессии должна быть больше 120. Составим и решим неравенство:
(n-15)(n+16)>0
+ - +
________ -16______0______15______
| //////////////////
n>15
По условию, число n должно быть минимальным.
Следовательно, n=16