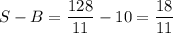В стране 100 городов: 30 из них находятся в горной части страны, а 70 — в равнинной. В течение трёх лет между городами устанавливали авиасообщение. Каждый год в стране открывалось 50 новых авиарейсов: все города случайным образом разбивались на 50 пар, и между городами из одной пары открывался рейс. Через три года оказалось, что из 150 открытых рейсов ровно 22 соединяют пару «горных» городов. Сколько рейсов соединяют пару «равнинных» городов?

Показать ответ

Ответ:

ketivolkowa

06.04.2022 14:44

ответ: Скорость-велосипедиста=300м/минуту,он ехал 15 минут,был и мотоциклист он ехал 800м/м спустя 9 минут мотоциклист догнал велосипедиста

Пошаговое объяснение:

нам понадобиться формула расчёта расстояния

S=v×t S-это расстояние V-это с какой скоростью едет, ну допустим мотоциклист .его V=800 T-это какое время объект ехал или шёл у велосипедиста это 15 минут. давайте решать!

узнаем сколько проехал велосипедист

S=300×15=4500(м)

Теперь узнаём методом подбора...и так я посчитал и подобрал число и это 9 и так проверяем

S=800×9=7200(м) вот мы узнали сколько проехал мотоциклист

Вы помните мы узнали сколько проехал велосипедист?Это нам сейчас пригодиться

S=300×9=2700(м)

(м)-метры

складываем 4500+2700=7200(м)

Вот! мотоциклист догнал велосипедиста и мы решили задачу

0,0(0 оценок)

Ответ:

Катя709015

10.01.2021 02:44

а) нет

б) нет

в) 18 / 11

Пошаговое объяснение:

Упорядочим числа по возрастанию (a₁ < a₂ < ... < a₁₁). Тогда по условию:

$\dfrac{a_1+a_2+...+a_6}{6}=7\Leftrightarrow a_1+a_2+...+a_6=42 \ (1)\\\dfrac{a_6+a_7+...+a_{11}}{6}=16\Leftrightarrow a_6+a_7+...+a_{11}=96\ (2)$

а) Если a₁ = 5, то a₂ ≥ 6, a₃ ≥ 7, ... a₆ ≥ 10. Тогда a₁ + a₂ + ... + a₆ ≥ 5 + 6 + ... + 10 = 45, но сумма шести наименьших чисел равна 42, она не может быть больше или равна 45. Значит, такое невозможно.

б) Если такое возможно, то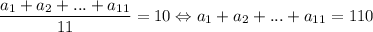 $\dfrac{a_1+a_2+...+a_{11}}{11}=10\Leftrightarrow a_1+a_2+...+a_{11}=110$

Сложим уравнения (1) и (2): a₁ + a₂ + ... + a₅ + 2a₆ + a₇ + ... + a₁₁ = 138. Но мы знаем, что a₁ + a₂ + ... + a₅ + a₆ + a₇ + ... + a₁₁ = 110. Тогда 110 + a₆ = 138 ⇔ a₆ = 28 ⇒ a₇ ≥ 29, a₈ ≥ 30, ... , a₁₁ ≥ 33 ⇒ a₆ + a₇ + ... + a₁₁ ≥ 28 + 29 + ... + 33 = 183. Минимально возможная сумма шести наибольших чисел в таком случае равна 183, что больше 96. Значит, такое невозможно.

в) Проведём действия, аналогичные пункту б): $\dfrac{a_1+a_2+...+a_{11}}{11}=S\Leftrightarrow a_1+a_2+...+a_{11}=11S$

a₁ + a₂ + ... + a₅ + 2B + a₇ + ... + a₁₁ = 138 ⇒ 11S + B = 138 ⇔ 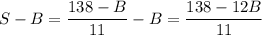$S=\dfrac{138-B}{11}$ ⇒ $S-B=\dfrac{138-B}{11}-B=\dfrac{138-12B}{11}$ . Данное выражение максимально при минимальном значении B.

Если a₆ = B, то в силу различности написанных чисел a₅ ≤ B - 1, a₄ ≤ B - 2, ... , a₁ ≤ B - 5. Тогда 42 = a₁ + a₂ + ... a₆ ≤ 6B - 15 ⇒ 6B ≥ 57 ⇔ B ≥ 9,5 ⇒ B ≥ 10. Тогда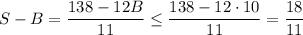 $S-B=\dfrac{138-12B}{11}\leq \dfrac{138-12\cdot 10}{11}=\dfrac{18}{11}$

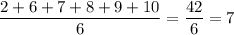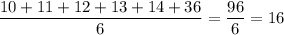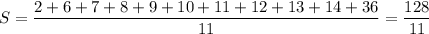Действительно, такое значение достигается, например, если были выписаны числа 2, 6, 7, 8, 9, 10, 11, 12, 13, 14, 36. Среднее арифметическое шести наименьших равно $\dfrac{2+6+7+8+9+10}{6}=\dfrac{42}{6}=7$ , среднее арифметическое шести наибольших равно $\dfrac{10+11+12+13+14+36}{6}=\dfrac{96}{6}=16$ , среднее арифметическое всех чисел $S=\dfrac{2+6+7+8+9+10+11+12+13+14+36}{11}=\dfrac{128}{11}$ , $S-B=\dfrac{128}{11}-10=\dfrac{18}{11}$