Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
Irina12345678901
14.12.2022 10:36 •
Математика
ТРУБЫ ГОРЯТ РЕШИТЕ ТРУБЫ ГОРЯТ РЕШИТЕ
Показать ответ
Ответ:
LiveRiot
15.10.2020 11:02
a)
b)
Тут явно
не выразить.
0,0
(0 оценок)
Популярные вопросы: Математика
dogsno
26.02.2022 07:58
Представте данную дробь в виде дроби со знаменателем 13 а)8/26 б)12/39 в)24/52 г) 30/65 представьте данную дробь в виде дроби со знаменателем 28 а) 1/4 б) 3/7 в)9/14...
пок15
26.02.2022 07:58
В6 а и 6 в классах 65 учащихся.в 6 а число девочек составляет 0,5 общего числа учащихся, а в 6 в-0,8этогочисла.сколько детей учится в каждом классе,если девочек в...
moyutot
26.02.2022 07:58
Сплав містить 4%срібла.скільки кілограм сплаву треба взяти щоб він мн містив 4,8кг срібла...
chunya20041
26.02.2022 07:58
Ширина прямоугольника 3 см.она на 20 мм меньше его длины.найди площадь прямоугольника?...
tural23
26.02.2022 07:58
Найдите закономерность и продолжите ряд: 1) 112 223 334 2) 776 555 334...
КириллFace
26.02.2022 07:58
Решить 2 двумя с одного аэродрома одновременно в противоположных направлениях вылетели два самолета.один летел со скоростью 748км/ч,другой-828км/ч.какое расстояние...
katyastulova23
26.02.2022 07:58
Впервый класс школы в этом году поступили 67 человек. их распределили по классам так: в 1а - 22 ученика, в 1б - столько же, в 1в - остальных детей. сколько учеников...
MokrovaDiana
24.08.2020 02:38
Две грузовых машины могут подойти на погрузку в промежуток времени от 10 до 11.30 часов. погрузка первой машины длится 10 минут, второй - 15 минут. какова вероятность,...
dddddkkke
24.08.2020 02:38
Уюры 43 наклейки, это на 27 наклеек меньше, чем у димы . сколько наклеек у димы?...
imbiz
24.08.2020 02:38
(признаки), указывающие на предстоящие явления погоды. ; .;...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
a)
b)
Тут явно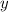 не выразить.
не выразить.