Товар в магазине стоил 3900руб. Сначала стоимость снизили на 30 процентов а потом повысили на 30 процентов Стоимость товара после снижения:
И конечная стоимость:

Показать ответ

Ответ:

mariarura

28.07.2021 19:03

Рок-му́зыка (англ. Rock music) — обобщающее название ряда направлений популярной музыки. Слово rock (в переводе с английского «качать», «укачивать», «качаться») в данном случае указывает на характерные для этих направлений ритмические ощущения, связанные с определённой формой движения, по аналогии с roll, twist, swing, shake… Такие признаки рок-музыки, как использование электромузыкальных инструментов, творческая самодостаточность (для рок-музыкантов характерно исполнение композиций собственного сочинения), являются вторичными и часто вводят в заблуждение. По этой причине принадлежность некоторых стилей музыки к року оспаривается.

0,0(0 оценок)

Ответ:

arturpushkin202453

08.06.2023 10:38

$F_0=0,F_1=1, F_n=F_{n-1}+F_{n-2}, n\in N\backslash\{1\}$

Заметим, что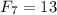 F_7=13

Докажем, что, начиная с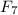 F_7 , последовательность Фибоначчи периодическая по модулю 1000.

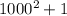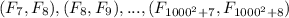Рассмотрим 1000^2+1 пару чисел $(F_7,F_8),(F_8,F_9),...,(F_{1000^2+7},F_{1000^2+8})$ .

Каждое из чисел каждой из пар дает один из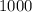 1000 остатков по модулю 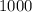1000 . Тогда всего вариантов пар остатков от деления на 1000 может быть 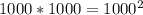1000*1000=1000^2 (1000 вариантов остатков 1ого числа пары и 1000 вариантов у 2ого).

Тогда, по принципу Дирихле, в рассматриваемом мн-ве пар найдутся хотя бы 2 пары чисел, соответствующие элементы которых сравнимы по модулю 1000 - а, с учетом определения последовательности Фибоначчи, это и означает периодичность остатков ее членов по модулю 1000.

Возьмем 2 такие пары с наименьшими номерами. Пусть это пары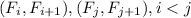 $(F_i,F_{i+1}), (F_j,F_{j+1}), i$ . Покажем, что i=7 .

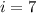Пусть не так, и .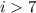

По построению,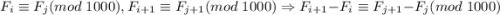 $F_i\equiv F_j(mod \;1000),F_{i+1}\equiv F_{j+1}(mod \;1000)\Rightarrow F_{i+1}-F_{i}\equiv F_{j+1}-F_{j}(mod \;1000)$

Но, по определению последовательности Фибоначчи,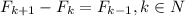 $F_{k+1}-F_{k}=F_{k-1},k\in N$ . А значит 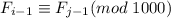$F_{i-1}\equiv F_{j-1}(mod\; 1000)$ . А тогда соответствующие элементы пар чисел 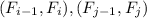$(F_{i-1},F_i),(F_{j-1},F_j)$ сравнимы по модулю 1000 - противоречие с тем, что 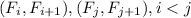$(F_i,F_{i+1}), (F_j,F_{j+1}), i$ - пары с наименьшими номерами.

Значит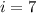 i=7 .

А это означает, что в последовательности остатков от деления членов последовательности Фибоначчи на 1000 найдется сколь угодно чисел, сравнимых с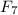 F_7 по модулю 1000. Т.к последовательность возрастающая и неограниченная, начиная со 2ого члена, это утверждение эквивалентно условию задачи.

Доказано.

________________________________

Можно доказать аналогичным образом и более общее утверждение: последовательность чисел Фибоначчи по модулю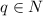 $q\in N$ периодическая (вышеприведенные рассуждения - частный случай этого док-ва). Длина периода такой последовательности обозначается 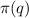$\pi(q)$ и называется период Пизано.