Пусть M и N – середины оснований BC и AD трапеции ABCD (AD > BC) и ∠A + ∠D = 90°. Через точку M проведём прямые, параллельные AB и CD. Пусть K и L – точки их пересечения с основанием AD. Тогда ∠MKL + ∠MLK = ∠A + ∠D = 90°. Поэтому ∠KML = 90°. Кроме того, NK = AN – AK = AN – BM = DN – CM = DN – DL = NL. Значит, MN – медиана прямоугольного треугольника KML, проведённая из вершины прямого угла. Поэтому 2MN = KL = AD – AK – LD = AD – BM – MC = AD – BC.
Через точку M проведём прямые, параллельные AB и CD. Пусть K и L – точки их пересечения с основанием AD. Тогда ∠MKL + ∠MLK = ∠A + ∠D = 90°. Поэтому ∠KML = 90°.
Кроме того, NK = AN – AK = AN – BM = DN – CM = DN – DL = NL. Значит, MN – медиана прямоугольного треугольника KML, проведённая из вершины прямого угла. Поэтому 2MN = KL = AD – AK – LD = AD – BM – MC = AD – BC.
Дано:
ABCD - трапеция
∠A+∠D=90°
BN=NC
AM=MD
Доказать: MN =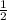 (AD+BC)
(AD+BC)
1) Построим NK || AB и NF || CD ABNK и NCDF параллелограммы.
2) ∠1 = ∠3 (Соответственные при AB || NK и секущей AK)
3) B ΔKNF: ∠3-∠4=90° => ∠N=90° и ΔKNF - прямоугольный, NM - медиана.
4) Следовательно, NM=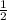 KF, где KF=AD - (AK-FD) = AD - BC => MN=
KF, где KF=AD - (AK-FD) = AD - BC => MN= 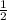 (AD-BC), что и требовалось доказать
(AD-BC), что и требовалось доказать