Основная логика решения заключаеться в том, что нам нужно упростить выражение, иначе мы его не посчитаем. Для этого можно присмотреться к степеням, и увидеть что они кратны 7 . Тогда получаеться:
1)
Так как у нас есть общая степень 7, то мы можем ее не учитывать при сравнении. Из этого следует, что нам нужно сравнивать:
2)
Если на этом этапе вы можете точно определить, какое число больше, значит задача решена, но для тех кто не уверен, можно пойти дальше. Выражения с обеих сторон можно представить в виде произведений с одинаковыми степенями:
3)
Теперь видно, что у нас есть пара степенных выражений с общим основанием, и мы можем их легко сравнить:
4)
Теперь мы знаем, что первая часть левого выражения больше первой правого. Дальше нам нужно сравнить вторые части обоих выражений, а тут уже нужно вспомнить таблицу умножения:
5)
Мы видим, что первое сравнение и второе не совпадают по знаку, тогда берем большее выражение из обоих неравенств и сравниваем между собой:
Пошаговое объяснение:
Основная логика решения заключаеться в том, что нам нужно упростить выражение, иначе мы его не посчитаем. Для этого можно присмотреться к степеням, и увидеть что они кратны 7 . Тогда получаеться:
1)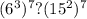
Так как у нас есть общая степень 7, то мы можем ее не учитывать при сравнении. Из этого следует, что нам нужно сравнивать:
2)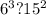
Если на этом этапе вы можете точно определить, какое число больше, значит задача решена, но для тех кто не уверен, можно пойти дальше. Выражения с обеих сторон можно представить в виде произведений с одинаковыми степенями:
3)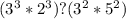
Теперь видно, что у нас есть пара степенных выражений с общим основанием, и мы можем их легко сравнить:
4)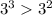
Теперь мы знаем, что первая часть левого выражения больше первой правого. Дальше нам нужно сравнить вторые части обоих выражений, а тут уже нужно вспомнить таблицу умножения:
5)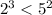
Мы видим, что первое сравнение и второе не совпадают по знаку, тогда берем большее выражение из обоих неравенств и сравниваем между собой:
6)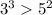
Из этого следует что: