События A и B независимы, причем P(A)=0,2 и P(B)=0,8.

Найдите вероятность события C=(A+B)⋅(A+B).

Показать ответ

Ответ:

Марат991

09.05.2023 11:34

Пошаговое объяснение:

Точка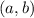 (a,b) на комплексной плоскости изображает число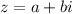 z =a+bi

$a = Re\ z$ - действительная часть числа (Real)

$b = Im\ z$ - мнимая часть числа (Imaginary)

В соответствии с этим строим точки для 16.1. (Картинка 1)

Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.

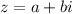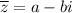Т.е. сопряженным для числа z =a+bi будет являться число $\overline{z} =a-bi$ .

В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).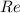

На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.

16.1 На комплексной плоскости постройте точки и еще 16.2

0,0(0 оценок)

Ответ:

ддииммоонн

09.10.2020 23:12

Вероятность того, что все 10 машин
будут в рабочем состоянии составляет:

$P_{10} = 0.9^{10} \ ;$

Вероятность того, что 9 машин будут в рабочем состоянии,
а одна – в ремонте, составляет:

$P_9 = 10 \cdot 0.1 \cdot 0.9^9 = 0.9^9 \ ,$
поскольку равновероятно в ремонте может оказаться первая машина, вторая машина, третья машина и т.д. до десятой.

Вероятность того, что 8 машин будут в рабочем состоянии,
а две – в ремонте, составляет:

$P_8 = C_{10}^2 \cdot 0.1^2 \cdot 0.9^8 = 0.45 \cdot 0.9^8 \ ,$
поскольку пара (из 10), оказавшаяся в ремонте может быть
составлена 45-тью $C_{10}^2 = \frac{ 10 \cdot 9 }{2} \ .$

Все эти вероятности описывают допустимые ситуации.
Искомая вероятность представляется их суммой:

$P = P_{10} + P_9 + P_8 = 0.9^{10} + 0.9^9 + 0.45 \cdot 0.9^8 = \\\\ = 0.9^8 ( 0.9^2 + 0.9 + 0.45 ) = 0.81^4 \cdot 2.16 \ = 0.9298091736 \ ;$

ответ: $P = 0.9298091736 \ ;$