Скільки різних натуральних чисел можеш скласти з циферблат 0.1.3.5.7 і якщо вони не повторюються

Показать ответ

Ответ:

friskdrimur

12.10.2022 01:15

Пошаговое объяснение:

48 см, 16 см, 30 см.

Пошаговое объяснение:

Пусть x см длина прямоугольного параллелепипеда. Тогда (3x) см его ширина , а высота (x+14) см . Сумма длин всех ребер прямоугольного параллелепипеда определяется по формуле : L =4*(a+b+c) , где а- длина , b-ширина , а с - высота прямоугольного параллелепипеда . 4∗(3x+x+x+14)=376;5x+14=376:4;5x+14=94;5x=94−14;5x=80;x=80:5;x=16.

Значит 16 см - ширина прямоугольного параллелепипеда.

16*3=48 см - длина .

16+14=30 см - высота.

Среднее арифметическое чисел - это сумма всех чисел, делённая на их количество.

Выражение: (8 × 4 - 6) : 5 = 5,2.

1) 8 × 4 = 32 - на столько увеличится сумма четырёх чисел;

2) 32 - 6 = 26 - на столько увеличится сумма пяти чисел;

3) 26 : 5 = 5,2 - на столько увеличится среднее арифметическое пяти чисел.

ответ: увеличится на 5,2.

0,0(0 оценок)

Ответ:

роолли

22.10.2020 14:23

$\dfrac{7}{66}$

Пошаговое объяснение:

Воспользуемся формулой числа сочетаний:

$C^m_n=\dfrac{n!}{(n-m)!\times m!}$

Тогда всего сочетаний:

$C^5_{11}=\dfrac{11!}{(11-5)!\times5!}=330$

Сочетаний, где хотя бы 4 книги - детективы:

$C^4_7=\dfrac{7!}{(7-4)!\times4!}=35$

Тогда ответом будет:

$P=\dfrac{35}{330}=\dfrac{7}{66}\approx0.1$

Задачу можно решить, не зная формулы выше, следующим

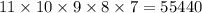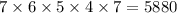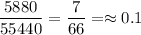Всего существует $11\times10\times9\times8\times7=55440$ комбинаций выбора 5-ти книг из 11 (здесь учитывается расположение каждой книги, поэтому числа получаются больше). $7\times6\times5\times4\times7=5880$ , случаев, которые подходят по условию. Откуда получили вероятность $\dfrac{5880}{55440}=\dfrac{7}{66}=\approx0.1$ .