Шар-пилот, объём которого равен 3600 дм³, наполнен гелием. Вычисли, какой подъёмной силой обладает шар. Плотность гелия равна 0,18кг/м³. Принять g=9,8Н/кг. Плотность воздуха считать равной 1,29кг/м³. Шар-пилот — аэростат, предназначенный для измерения скорости ветра.

Показать ответ

Ответ:

katecat20171

03.12.2020 10:00

26.

Всего транспортных средств - 25

Автобусов - 16

Значит вероятность: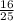 $\frac{16}{25}$ = 0,64

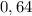
ответ: 0,64

27.

Всего ученых - 10

Из России - 3

Вероятность: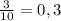 $\frac{3}{10} = 0,3$

ответ: 0,3

28.

Всего холодильников - 2 000

С браком - 5

Вероятность: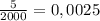 $\frac{5}{2 000} = 0,0025$

ответ: 0,0025

29.

3 300 - 100%

х - 10%

х = 3 300 * 10 / 100 = 330 руб. - сборка.

3 300 + 330 = 3 630 руб. - стоимость шкафа со сборкой.

ответ: 3 630 рублей.

30.

360 - 300 = 60 руб. - подорожала.

300 - 100%

60 - х

х = 60 * 100 / 300 = 20%

ответ: на 20%

31.

х - 100%

23 - 92%

х = 23 * 100 / 92 = 25 выпускника - всего сдавали экзамен по русскому языку.

25 - 23 = 2 выпускника - не сдали экзамен.

ответ: 2 выпускника.

0,0(0 оценок)

Ответ:

06Sofa07

31.10.2022 11:50

Дано:

△ABC - равнобедренный;

P△ABC = 36, AB = 16.

Найти:

S△ABC = ? (ед. кв).

Решение:

Т.к. △ABC - равнобедренный ⇒ AC = CB, по свойству равнобедренного тр-ка.

Предположим, что основание составляет 16. Тогда:

AC = CB = (36 - 16) : 2 = 20 : 2 = 10.

Проверим, верно ли это по теореме о неравенстве тр-ка.

"Каждая сторона треугольника меньше суммы двух других сторон".

⇒ 16 + 10 > 10, 10 + 10 > 16, 10 + 16 > 16 (всё совпадает, поэтому боковую сторону и основание мы нашли верно).

Формула площади треугольника выглядит следующим образом:

S△ = 1/2 ⋅ a ⋅ h, где a - основание (AB), h - высота.

Проведём из точки B к основанию равнобедренного тр-ка высоту CH. При этом у нас образовалось два равных прямоугольных треугольника ACH и BCH (их равенство можно доказать по всем признакам равенства прямоугольных тр-ков, исходя из того, что △ABC - равнобедренный).

"В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой".

⇒ CH является медианой и делит основание AB так, что AH = HB = 16 : 2 = 8.

Найдём высоту равнобедренного тр-ка ABC по теореме Пифагора (a = √(c² - b²), где a и b - катеты, c - гипотенуза).

CH = √(AC² - AH²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

CH = √(CB² - HB²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

Найдём площадь равнобедренного тр-ка ABC по указанной выше формуле:

S△ABC = 1/2 ⋅ 16 ⋅ 6 = 16/2 ⋅ 6 = 8 ⋅ 6 = 48 (ед. кв).

ответ: 48 (ед. кв).
ABC-равнобедренний треугольникP=36AB=16Ниайдите Площадь