с заданием по Литературе 6 класс . *извините нажала не туда по этому стоит тема математика * Напишите, какое впечатление произвели на вас персонажи пьесы "Обыкновенное чудо "? Кто вызвал у вас симпатию, а кто, напротив, неприятные чувства? Почему?
ответ: задача имеет два варианта решения, Вася мог задумать 14 или 12.
Пошаговое объяснение:
По условию задачи Вася задумал целое число; Коля умножил его не то на 5, не то на 6; Женя прибавил к результату Коли не то 5, не то 6; Саша отнял от результата Жени не то 5, не то 6; в итоге получилось 71. Чтобы узнать, какое число задумал Вася, рассмотрим все варианты возможных решений и определим те, которые соответствуют заданному условию.
Рассмотрим случай, если задуманное число умножили на 5
Обозначим задуманное число Х, тогда можно составить следующий ряд уравнений.
Первый вариант: если к умноженному на 5 задуманному числу прибавили 5 и отняли 5:
5 * Х + 5 - 5 = 71;
5Х = 71;
Х = 71 / 5 = 14,2; такое решение невозможно, так как задуманное число — целое.
Второй вариант: если к умноженному на 5 задуманному числу прибавили 5 и отняли 6:
5 * Х + 5 - 6 = 71;
5Х - 1 = 71;
5Х = 72;
Х = 72 / 5 = 14,5; такое решение невозможно, так как задуманное число — целое.
Третий вариант: если к умноженному на 5 задуманному числу прибавили 6 и отняли 5:
5 * Х + 6 - 5 = 71;
5Х + 1 = 71;
5Х = 71 - 1
Х = 70 / 5 = 14, возможное решение.
Четвертый вариант: если к умноженному на 5 задуманному числу прибавили 6 и отняли 6:
5 * Х + 6 - 6 = 71;
5Х = 71;
Х = 71 / 5 = 14,2, такое решение невозможно, так как задуманное число — целое.
Рассмотрим случай, если задуманное число умножили на 6
Обозначим задуманное число Y, тогда можно составить следующий ряд уравнений.
Первый вариант: если к умноженному на 6 задуманному числу прибавили 5 и отняли 5:
6 * Y + 5 - 5 = 71;
6Y = 71;
Y = 71 / 6 = 11 5/6; такое решение невозможно, так как задуманное число — целое.
Второй вариант: если к умноженному на 6 задуманному числу прибавили 5 и отняли 6:
6 * Y + 5 - 6 = 71;
6Y - 1 = 71;
6Y = 72;
Y = 72 / 6 = 12; возможное решение.
Третий вариант: если к умноженному на 6 задуманному числу прибавили 6 и отняли 5:
6 * Y + 6 - 5 = 71;
6Y + 1 = 71;
6Y = 71 - 1
Y = 70 / 6 = 11 3/ 6, такое решение невозможное, так как задуманное число — целое.
Четвертый вариант: если к умноженному на 6 задуманному числу прибавили 6 и отняли 6:
6 * Y + 6 - 6 = 71;
6Y = 71;
Y = 71 / 6 = 11 5/6, такое решение невозможно, так как задуманное число — целое.
Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:
Необходимо найти касательную к графику функции , проходящую через точку .
Пусть - точка касания. Уравнение касательной:
Найдем производную:
Подставим все величины в уравнение касательной:
Поскольку касательная проходит через точку , то подставим координаты этой точки в уравнение:
Значит, уравнение касательной имеет вид:
Полуокружность , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
Таким образом, две касательные задаются уравнением:
ответ: задача имеет два варианта решения, Вася мог задумать 14 или 12.
Пошаговое объяснение:
По условию задачи Вася задумал целое число; Коля умножил его не то на 5, не то на 6; Женя прибавил к результату Коли не то 5, не то 6; Саша отнял от результата Жени не то 5, не то 6; в итоге получилось 71. Чтобы узнать, какое число задумал Вася, рассмотрим все варианты возможных решений и определим те, которые соответствуют заданному условию.
Рассмотрим случай, если задуманное число умножили на 5
Обозначим задуманное число Х, тогда можно составить следующий ряд уравнений.
Первый вариант: если к умноженному на 5 задуманному числу прибавили 5 и отняли 5:
5 * Х + 5 - 5 = 71;
5Х = 71;
Х = 71 / 5 = 14,2; такое решение невозможно, так как задуманное число — целое.
Второй вариант: если к умноженному на 5 задуманному числу прибавили 5 и отняли 6:
5 * Х + 5 - 6 = 71;
5Х - 1 = 71;
5Х = 72;
Х = 72 / 5 = 14,5; такое решение невозможно, так как задуманное число — целое.
Третий вариант: если к умноженному на 5 задуманному числу прибавили 6 и отняли 5:
5 * Х + 6 - 5 = 71;
5Х + 1 = 71;
5Х = 71 - 1
Х = 70 / 5 = 14, возможное решение.
Четвертый вариант: если к умноженному на 5 задуманному числу прибавили 6 и отняли 6:
5 * Х + 6 - 6 = 71;
5Х = 71;
Х = 71 / 5 = 14,2, такое решение невозможно, так как задуманное число — целое.
Рассмотрим случай, если задуманное число умножили на 6
Обозначим задуманное число Y, тогда можно составить следующий ряд уравнений.
Первый вариант: если к умноженному на 6 задуманному числу прибавили 5 и отняли 5:
6 * Y + 5 - 5 = 71;
6Y = 71;
Y = 71 / 6 = 11 5/6; такое решение невозможно, так как задуманное число — целое.
Второй вариант: если к умноженному на 6 задуманному числу прибавили 5 и отняли 6:
6 * Y + 5 - 6 = 71;
6Y - 1 = 71;
6Y = 72;
Y = 72 / 6 = 12; возможное решение.
Третий вариант: если к умноженному на 6 задуманному числу прибавили 6 и отняли 5:
6 * Y + 6 - 5 = 71;
6Y + 1 = 71;
6Y = 71 - 1
Y = 70 / 6 = 11 3/ 6, такое решение невозможное, так как задуманное число — целое.
Четвертый вариант: если к умноженному на 6 задуманному числу прибавили 6 и отняли 6:
6 * Y + 6 - 6 = 71;
6Y = 71;
Y = 71 / 6 = 11 5/6, такое решение невозможно, так как задуманное число — целое.
Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:
Необходимо найти касательную к графику функции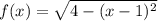 , проходящую через точку
, проходящую через точку 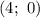 .
.
Пусть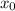 - точка касания. Уравнение касательной:
- точка касания. Уравнение касательной:
Найдем производную:
Подставим все величины в уравнение касательной:
Поскольку касательная проходит через точку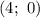 , то подставим координаты этой точки в уравнение:
, то подставим координаты этой точки в уравнение:
Значит, уравнение касательной имеет вид:
Полуокружность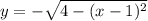 , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
, расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
Таким образом, две касательные задаются уравнением: