Решите уравнение в натуральных числах
(a-2020)*(b+2021)=2022

168 см²

Пошаговое объяснение:

Треугольник равнобедренный.

Проведём высоту, к основанию, эта высота будет также медианой, и поделит основание АС пополам.

По теореме Пифагора найдем высоту.

h²=BC²-(AC/2)²=25²-7²=625-49=576 см

h=√576=24 см.

S=1/2*h*AC=24*14/2=168 см² площадь треугольника.

ответ:168см² площадь треугольника

По формуле Герона.

S=√(p(p-AB)(p-BC)(p-AC)), где р- полупериметр.

р=(АВ+ВС+АС)/2=(25+25+14)/2=64/2=32 см полупериметр треугольника.

S=√(32(32-25)(32-25)(32-14))=

=√(32*7*7*18)=7√(4*4*2*2*3*3)=7*4*2*3=168 см² площадь треугольника

324, 648.

Пошаговое объяснение:

Пусть в числе k цифр. Максимально возможная сумма цифр - это 9k, тогда само число не больше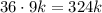 . При этом само число не меньше 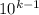. Чтобы был хоть какой-то шанс найти k-значное число, удовлетворяющее условию, должно быть выполнено неравенство .

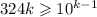Правая часть неравенства растёт гораздо быстрее левой. Подбором находим, что при k = 4 неравенство выполнено, а при k = 5 уже нет. Докажем, что и при всех больших k неравенство не выполнено, по индукции:

База. k = 5: Переход. Пусть для всех 4 < k < n выполнено . Докажем, что и для k = n это так. Действительно, при n > 4

Сумма цифр принимает значения вплоть до 36. Для сокращения перебора вспомним, что если число делится на 9 (а оно делится, так как делится на 36), то и сумма цифр должна делиться. Остаются 4 варианта:

Сумма цифр 9, тогда само число должно быть . У него сумма цифр 9, подходит.Сумма цифр 18, само число , сумма цифр правильная, подходит.Сумма цифр 27, само число , не подходитСумма цифр 36, само число , не подходит.