Решите .товар коштував 200 грн.першого разу його ціна знизилась на 10%, а друга на 18 грн.на скільки відсотків знизилась ціна товару другого разу/

Показать ответ

Ответ:

Pahamoseuv

02.02.2023 18:49

Пусть угол BAL равен альфа , угол ACB равен бета . Сумма углов в треугольнике ABC равна 180°, откуда 2 альфа плюс 31 градусов плюс бета =180 градусов. Аналогично, из треугольника ALC альфа плюс 58 градусов плюс бета =180 градусов. Получаем систему уравнений:
система выражений новая строка 2 альфа плюс 31 градусов плюс бета =180 градусов, новая строка альфа плюс 58 градусов плюс бета =180 градусов конец системы равносильно система выражений новая строка 2(122 градусов минус бета ) плюс бета =149 градусов, новая строка альфа =122 градусов минус бета конец системы равносильно система выражений новая строка бета =95 градусов, новая строка альфа =27 градусов. конец системы
Таким образом, угол ACB равен 95°.

Ответ: 95.

0,0(0 оценок)

Ответ:

jeon200

24.07.2020 23:28

Вероятность события "монета выпала решкой ровно 10 раз" больше вероятности события "монета выпала решкой ровно 13 раз" в 14,3 раза.

Объяснение:

Определить, во сколько раз вероятность события "монета выпала решкой ровно 10 раз" больше вероятности события "монета выпала решкой ровно 13 раз".

1) Введем обозначения по условию:

Число бросков n = 16:

1-е событие "монета выпала решкой ровно 10 раз" k = 10;

2-е событие "монета выпала решкой ровно 13 раз" k = 13.

Найти отношение вероятности первого события ко второму:

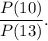
$\displaystyle \frac {P(10)}{P(13)}.$

Вероятностью наступления некоторого события называется отношение числа благоприятных исходов к числу всех возможных исходов.

2) При бросании монеты число всех исходов равно 2ⁿ.

В нашем случае число всех возможных исходов одной или другой стороны монеты при 16 бросках равно 2¹⁶.

Число сочетаний без повторений из n элементов по k - это количество , которыми можно выбрать k элементов из n без учета порядка.

$\displaystyle C^{k} _{n} = \frac{n!}{k! (n-k)!}$

3) Число благоприятных исходов в первом случае.

Число бросков n = 16

Число выпадений решки k = 10.

Число благоприятных исходов в первом случае равно числу сочетаний из 16 по 10.

$\displaystyle C^{k} _{n} = \frac{16!}{10! (16-10)!}= \frac{16!}{10! \cdot 6!}.$

4) Вероятность события "монета выпала решкой ровно 10 раз".

$\displaystyle P(10) = \frac{C^{10}_{16}}{2^{16}} = \frac{16!}{10! \cdot 6! \cdot 2^{16} } .$

5) Число благоприятных исходов во втором случае.

Число бросков n = 16

Число выпадений решки k = 13.

Число благоприятных исходов во втором случае равно числу сочетаний из 16 по 13.

$\displaystyle C^{k} _{n} = \frac{16!}{13! (16-13)!}= \frac{16!}{13! \cdot 3!}.$

6) Вероятность события "монета выпала решкой ровно 13 раз"

$\displaystyle P(13) = \frac{C^{13}_{16}}{2^{16}} = \frac{16!}{13! \cdot 3! \cdot 2^{16} } .$

7) Найдем, во сколько раз вероятность первого события больше вероятности второго события.

$\displaystyle \frac{P(10)}{P(13)} =\frac{C^{10}_{16}}{2^{n}} : \frac{C^{13}_{16}}{2^{n}} =\frac{C^{10}_{16}}{2^{n}} \cdot \frac{2^{n}}{C^{13}_{16}} =\frac{C^{10}_{16}}{C^{13}_{16}} .$

$\displaystyle \frac{P(10)}{P(13)} =\frac{16! \cdot 13! \cdot 3!}{10! \cdot 6! \cdot 16!} =\frac{10! \cdot 11 \cdot 12 \cdot 13 \cdot 3!}{10! \cdot 3! \cdot 4 \cdot 5 \cdot 6} =\\\\\\=\frac{11 \cdot 13}{10} = \frac{143}{10} =14,3$