Чтобы найти критическую точку, нужно найти такие , при которых функция (производная ) равна 0.
Будем пользоваться формулой производной произведения: и производной сложной функции: .
В нашем случае: . Приравниваем к 0: , так как . При этом если , то производная положительна, а если , то производная отрицательна. Значит, — точка максимума.
Чтобы найти критическую точку, нужно найти такие , при которых функция
, при которых функция 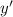 (производная
(производная 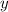 ) равна 0.
) равна 0.
Будем пользоваться формулой производной произведения: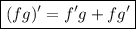 и производной сложной функции:
и производной сложной функции: ![\boxed{[f(g(x))]'=f'(g(x))\times g'(x)}](/tpl/images/1358/2008/9d433.png) .
.
В нашем случае: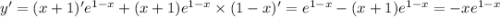 . Приравниваем к 0:
. Приравниваем к 0: 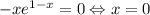 , так как
, так как 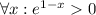 . При этом если
. При этом если 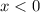 , то производная положительна, а если
, то производная положительна, а если 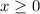 , то производная отрицательна. Значит,
, то производная отрицательна. Значит, 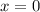 — точка максимума.
— точка максимума.