решить задачу на множества! Известно, что из N учеников спортом увлекаются A учеников, программированием B, математикой C, спортом и программированием D, спортом и математикой E, программированием и математикой F, спортом, математикой и программированием G учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
N=100, A=35, B=30, C=40, D=12, E=10, F=8, G=5
Пошаговое объяснение:
В каждое из множеств D, E и F входит подмножество G, поэтому только спортом и программированием (но не математикой) увлекаются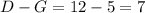 человек, только спортом и математикой (но не программированием) увлекаются
человек, только спортом и математикой (но не программированием) увлекаются 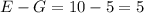 человек, только программированием и математикой (но не спортом) увлекаются
человек, только программированием и математикой (но не спортом) увлекаются 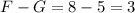 человека.
человека.
Поскольку в множество A помимо учеников, увлекающихся только спортом, входят также подмножества D и E, а также их пересечение G, то количество увлекающихся только спортом можно вычислить как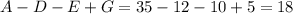 человек. Аналогично, только программированием увлекаются
человек. Аналогично, только программированием увлекаются 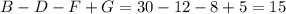 человек, только математикой увлекаются
человек, только математикой увлекаются 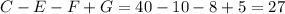 человек.
человек.
Количество учеников, которые увлечены хотя бы чем-то, можно вычислить как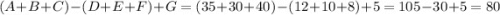 человек, следовательно ничем не увлекаются
человек, следовательно ничем не увлекаются  человек.
человек.