Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
yanakorzh2003
23.01.2020 18:05 •
Математика
решить.Математика 1 курс
Показать ответ
Ответ:
inferatu777
16.07.2021 02:35
1.
2.
3.
1.
2.
3.
4.
5.
6.
4.
5.
1.
2.
3.
4.
5.
6.
0,0
(0 оценок)
Популярные вопросы: Математика
mirakle1
02.09.2020 08:37
Поострой в гоординатной плоскрсти отрезок СD если C(-3:-2),D(0:4)...
kocheryan86p08jni
02.09.2020 08:37
В банке лежат 6 пакетиков с зеленым чаем и 8 пакетиков с черным чаем. Пакетики берут из банки по 2 штуки. Если взяли одинаковые пакетики,то в банку кладут пакетик с черным чаем....
ЛамповаяУмничка
19.02.2022 15:49
. Крыша имеет форму пирамиды, основание которой – прямоугольник со сторонами a и b, боковые ребра равнонаклонены к основанию под углом β. Сколько листов железа размером 0,70×1,4...
alexnn08
19.02.2022 15:49
Подайте у вигляді степеня з основою х вираз...
oleh09156
16.04.2021 01:08
Площадь прямоугольника 288 см а периметр 72 какая длина сторон прямоугольника...
Tima66666666
16.04.2021 01:08
Вместо знаков вопроса поставьте числа чтобы получились верные записи. 8м+3дм = ? м ? дм...
Полина200618
16.04.2021 01:08
Блин найдите больший угол равнобедренной трапеции авсд если диагональ ас образует с основанием ад и боковой стороной ав углы равные 46 и 1 соответственно .ответ дайте в градусах....
petrovspb
16.04.2021 01:08
Саша ходит в бассейн один раз в три дня, коля раз в 4 дня,петя раз в 5 дней. мальчики встретились в бассейне во вторник. через сколько дней в какой день недели они встретиться в...
Eldar1001
16.04.2021 01:08
Запиши число, в котором 1 сотня; запиши число, в котором 10 сотен. выпиши из данных чисел только те, которые относятся к «круглым» тысячам. 3000, 5300, 6700, 10000, 5000, 9800,...
НастёнышЬ14
25.09.2020 08:50
Заполни магические квадраты 270 260 250 230...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
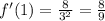
2.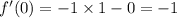
3.1.
2.
3.
4.
5.
6.

4.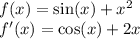
5.1.
2.
3.
4.
5.
6.