так как
Неравенство принимает вид
Логарифмическая функция с основанием 3 возрастает, большему значению функции соответствует большее значение аргумента
и учитывая область определения логарифмической функции получаем
систему двух неравенств:
Решения второго неравенства входят в первое, поэтому решаем первое:
Квадратное неравенство относительно
Замена переменной:
D=81-32=49
⇒ 0 < t ≤1 или t ≥8
Обратная замена:
0 < ≤1 или ≥8
x ≤1 или x ≥ log₄8=3/2
О т в е т. (-∞;1} U {1,5; +∞)
так как
Неравенство принимает вид
Логарифмическая функция с основанием 3 возрастает, большему значению функции соответствует большее значение аргумента
и учитывая область определения логарифмической функции получаем
систему двух неравенств:
Решения второго неравенства входят в первое, поэтому решаем первое:
Квадратное неравенство относительно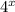
Замена переменной:
D=81-32=49
Обратная замена:
0 <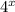 ≤1 или
≤1 или 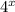 ≥8
≥8
x ≤1 или x ≥ log₄8=3/2
О т в е т. (-∞;1} U {1,5; +∞)