Домножаем левую и правую частей уравнений на для до того, чтобы в левой части уравнения применить формулу дифференцирования произведения двух функций.
Далее решается стандартное дифференциальное уравнение. Интегрируется по обеим частям
Пробуйте найти интеграл сами, никак не берётся.
Домножаем левую и правую частей уравнений на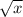 для до того, чтобы в левой части уравнения применить формулу дифференцирования произведения двух функций.
для до того, чтобы в левой части уравнения применить формулу дифференцирования произведения двух функций.
Далее решается стандартное дифференциальное уравнение. Интегрируется по обеим частям
Пробуйте найти интеграл сами, никак не берётся.