В коробке 8 жуков и пауков всего у них 54 ноги сколько вкоробке жуков и сколько пауков? У жука 6 лапок, у паука 8 лапок.
Если взять паука и жука, то у них вместе 6+8 = 14 лапок.
Если разделить 54 на 14, то получится 3 и 12 в остатке. (54=14*3+12)
Значит в коробке минимум 3 паука. у трех пауков 3*8-24 лапки. Осталось 54-24=30 лапок - это в точности 5*6, то есть в коробке 3 паука и 5 жуков.
На самом деле можно и прямым перебором выйти на это же число, предполагая, что в коробке 1 паук и 7 жуков - посчитать по лапкам и понять, что на 54 лапки не выйти, так же проверить 2 паука и 6 жуков и тд до 7 пауков и 1 жука - подойбет только вариант 3 паука и 5 жуков
коробке 3 паука и 5 жуков.
Пошаговое объяснение:
В коробке 8 жуков и пауков всего у них 54 ноги сколько вкоробке жуков и сколько пауков? У жука 6 лапок, у паука 8 лапок.
Если взять паука и жука, то у них вместе 6+8 = 14 лапок.
Если разделить 54 на 14, то получится 3 и 12 в остатке. (54=14*3+12)
Значит в коробке минимум 3 паука. у трех пауков 3*8-24 лапки. Осталось 54-24=30 лапок - это в точности 5*6, то есть в коробке 3 паука и 5 жуков.
На самом деле можно и прямым перебором выйти на это же число, предполагая, что в коробке 1 паук и 7 жуков - посчитать по лапкам и понять, что на 54 лапки не выйти, так же проверить 2 паука и 6 жуков и тд до 7 пауков и 1 жука - подойбет только вариант 3 паука и 5 жуков
Пошаговое объяснение:
Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).
Решать задачу будем следующим образом:
вспомним формулу для нахождения расстояния между точками на плоскости;
обозначим точки равноудаленные от А и В координатами (x; y);
запишем расстояния между точкой А и (x; y);
запишем расстояние между точками B и (x; y);
приравняем расстояния и выразим одну переменную через другую.
Вспомним формулу для нахождения расстояния на плоскости
Формула для нахождения расстояния между точками на плоскости выглядит так:
AB =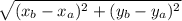
, где точки А и В заданы координатами A и B
Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).
Составим уравнение геометрического места точек
Записываем расстояние между точкой A (2; -3) и (x; y):
Записываем расстояние между точками B (-4; 1) и (x; y):
Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:
Открываем скобки, переносим все слагаемые в право и приводим подобные.
или