Решить, ! ! 49 ! нужно найти целые положительные a, b, c, d, не превосходящие 17^11 и удовлетворяющие условию если решений несколько, принимается любое. a/b+c/d=1 a/d+c/b=2018
Тут, скорее, подойдёт метод пристального взгляда, с которого можно подобрать какие-то решения (это я к тому, чтобы не спрашивали, откуда взялись именно такие решения, всё методом проб и ошибок). Возьмём b = 2018k, d = ab, c ⋮ a, c / a = m. Тогда в первом уравнении получится . Во втором уравнении получаем . Чтобы легче было считать, возьмём k квадратом какого-нибудь числа. Если k = 1, то b = 2018, c = 2017 * 2019, a = 2017 или 2019. Уже отсюда видим, что a + m = 2017 + 2019 > 2018. Возьмём k = 4: b = 8072, c = 4035 * 4037, a = 4037 (оставим это), d = 4037 * 8072. Тогда для первого уравнения - верно. Для второго: - верно. Таким образом, четвёрка a = 4037, b = 8072, c = 4035 * 4037, d = 4037 * 8072 нам подходит.
a = 4037, b = 8072, c = 16289295, d = 32586664
Тут, скорее, подойдёт метод пристального взгляда, с которого можно подобрать какие-то решения (это я к тому, чтобы не спрашивали, откуда взялись именно такие решения, всё методом проб и ошибок). Возьмём b = 2018k, d = ab, c ⋮ a, c / a = m. Тогда в первом уравнении получится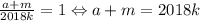 . Во втором уравнении получаем
. Во втором уравнении получаем  . Чтобы легче было считать, возьмём k квадратом какого-нибудь числа. Если k = 1, то b = 2018, c = 2017 * 2019, a = 2017 или 2019. Уже отсюда видим, что a + m = 2017 + 2019 > 2018. Возьмём k = 4: b = 8072, c = 4035 * 4037, a = 4037 (оставим это), d = 4037 * 8072. Тогда для первого уравнения
. Чтобы легче было считать, возьмём k квадратом какого-нибудь числа. Если k = 1, то b = 2018, c = 2017 * 2019, a = 2017 или 2019. Уже отсюда видим, что a + m = 2017 + 2019 > 2018. Возьмём k = 4: b = 8072, c = 4035 * 4037, a = 4037 (оставим это), d = 4037 * 8072. Тогда для первого уравнения 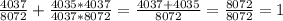 - верно. Для второго:
- верно. Для второго: 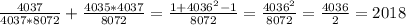 - верно. Таким образом, четвёрка a = 4037, b = 8072, c = 4035 * 4037, d = 4037 * 8072 нам подходит.
- верно. Таким образом, четвёрка a = 4037, b = 8072, c = 4035 * 4037, d = 4037 * 8072 нам подходит.