Расстояние между двумя пристанями по реке равно 12 км. за 7 часов лодка проплыла от одной пристани до другой и вернулась обратно. известно, что собственная скорость лодки 5 км/ч. найдите скорость течения реки. обозначьте буквой х скорость течения реки (в км/ч) и составьте уравнение по условию . решение запишите.
Пусть скорость течения реки равна х км/ч, тогда скорость против течения - (5-x) км/ч, а по течению - (5+x) км/ч. Время, затраченное лодкой против течения равно 12/(5-x)ч, а по течению - 12/(5+x) ч. На весь путь лодка затратила 12/(5-x) + 12/(5+x), что по условию составляет 7 часов.
Составим уравнение
Пусть х - скорость течения реки.
Тогда :
(5 + х) км/ч - скорость лодки по течению реки
(5 - х) км/ч - скорость лодки против течения реки
Весь путь туда/обратно лодка проплыла за 7 часов.
Уравнение
120 = 7(25 - x²) ⇔ 120 = 175 - 7x² ⇔ 7x² = 55
x ≈ 2,8 км/ч
ответ: скорость течения реки равна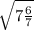 км/ч ≈ 2,8 км/ч
км/ч ≈ 2,8 км/ч