Для построения нужны: линейка, чертежный треугольник ( как известно, он имеет форму прямоугольного треугольника), карандаш. –––––––––––– Начертите произвольный треугольник - какой Вам нравится. К одной из его сторон приложите угольник так, чтобы его катет совпал со стороной нарисованного треугольника - как показано на рисунке, данном в приложении. К стороне угольника - гипотенузе- приложите линейку. Сдвигайте угольник по линейке так, чтобы катет, совпадавший со стороной треугольника, оказался у противоположной той стороне вершине. Чертите по катету прямую. Она будет параллельна стороне. Точно так же начертите прямые, параллельные двум другим сторонам треугольника. ––––––––––– Таким не сдвигая линейку с места, можно начертить сколько угодно прямых, параллельных данной.
––––––––––––
Начертите произвольный треугольник - какой Вам нравится.
К одной из его сторон приложите угольник так, чтобы его катет совпал со стороной нарисованного треугольника - как показано на рисунке, данном в приложении.
К стороне угольника - гипотенузе- приложите линейку. Сдвигайте угольник по линейке так, чтобы катет, совпадавший со стороной треугольника, оказался у противоположной той стороне вершине. Чертите по катету прямую. Она будет параллельна стороне.
Точно так же начертите прямые, параллельные двум другим сторонам треугольника.
–––––––––––
Таким не сдвигая линейку с места, можно начертить сколько угодно прямых, параллельных данной.
(см. объяснение)
Пошаговое объяснение:
Выполним замену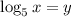 . Тогда
. Тогда 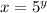 .
.
Заметим сразу, что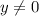 , так как
, так как 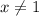 .
.
Тогда уравнение примет вид:
Так как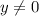 , то верно, что
, то верно, что 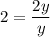 .
.
С учетом этого перепишем уравнение:
Тогда перейдем к совокупности:
Рассмотрим первую строку совокупности:
Слева показательная функция. Она монотонно возрастает.
Справа гипербола. Она убывает на всей области определения.
Тогда рассматриваемое уравнение может иметь не более одного корня.
Несложно увидеть, что это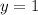 , так как при нем равенство верно.
, так как при нем равенство верно.
Рассмотрим вторую строку совокупности:
Выполним теперь обратную замену:
Так, учитывая ОДЗ, мы получили, что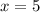 и
и 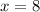 - это корни исходного уравнения.
- это корни исходного уравнения.
Задание выполнено!