Эту задачу можно решить двумя
1) геометрическим,
2) векторным.
1) Примем сторону основания а = 1 (как дано в задании), боковое ребро = √19 .
В осевом сечении ASD проекция отрезка АМ на основание равна 1,5.
Высота пирамиды Н = √((√19)² - 1²) = √18 = 3√2.
Высота точки М равна половине этой величины, то есть 3√2/2.
Отрезок АМ пересекает высоту SO в точке Е.
Проекция ЕМ на горизонт равна (1/3) проекции АМ, то есть 1,5/3 = 0,5.
Проекция ЕМ на вертикаль равна (1/3) высоты точки М, то есть (3√2/2)/3 = √2/2.
Угол между ЕМ и плоскостью СSF и есть искомый угол.
ЕM = 1/cos 30° = 1/(√3/2) = 2/√3 = 2√3/3.
Расстояние от точки М до плоскости СSF равно 0,5*sin 60° = √3/4.
Отсюда находим искомый угол α:
sin α = (√3/4)/(√3/2) = 1/2.
α = arc sin (1/2) = 30°.
2) Поместим пирамиду в систему координат вершиной A в точку √3/2, ребром ВС по оси Оу.
Координаты точек:
C(0; 1,5; 0), S(√3/2; 1; 3√2), F(√3; 0,5; 02).
По трём точкам находим уравнение плоскости ASC:
ASC: 5,19615x + 9y + 0z - 13,5 = 0 .
Точки A(√3/2; 0; 0), M(√3/2; 1; 3√2).
Вектор MA: (0; 1,5; 3√2/2).
Направляющий вектор прямой имеет вид: l m n
Скалярное произведение 13,5
s = {l; m; n} 0 1,5 2,12132
Модуль = √6,75 = 2,598.
Вектор нормали плоскости имеет вид:
A B C sin fi = 0,5
Ax + By + Cz + D = 0 5,196152423 9 0
Модуль 10,3923.
fi = 0,5236 радиан = 30 градус .
Так как каждый пункт рассматривается в качестве отдельной задачи, замечательные точки треугольника всегда будут называться O.
а) BM₂ точкой пересечения медиан делится в отношении BO : OM₂ = 2 : 1 ⇒ .
Так как AB = BC, BM₂ — высота. По теореме Пифагора .
Тогда
б) Точка пересечения биссектрис — центр вписанной окружности. Так как AB = BC, BB₂ — высота ⇒ OB₂ — радиус (r) вписанной окружности.
Площадь треугольника ABC
в) Точка пересечения серединных перпендикуляров — центр описанной окружности ⇒ OB — радиус (R) описанной окружности. Площадь треугольника ABC
г) Площадь треугольника ABC
ответ: а) 8; б) 7,5; в) 9,375; г) 5,25
Эту задачу можно решить двумя
1) геометрическим,
2) векторным.
1) Примем сторону основания а = 1 (как дано в задании), боковое ребро = √19 .
В осевом сечении ASD проекция отрезка АМ на основание равна 1,5.
Высота пирамиды Н = √((√19)² - 1²) = √18 = 3√2.
Высота точки М равна половине этой величины, то есть 3√2/2.
Отрезок АМ пересекает высоту SO в точке Е.
Проекция ЕМ на горизонт равна (1/3) проекции АМ, то есть 1,5/3 = 0,5.
Проекция ЕМ на вертикаль равна (1/3) высоты точки М, то есть (3√2/2)/3 = √2/2.
Угол между ЕМ и плоскостью СSF и есть искомый угол.
ЕM = 1/cos 30° = 1/(√3/2) = 2/√3 = 2√3/3.
Расстояние от точки М до плоскости СSF равно 0,5*sin 60° = √3/4.
Отсюда находим искомый угол α:
sin α = (√3/4)/(√3/2) = 1/2.
α = arc sin (1/2) = 30°.
2) Поместим пирамиду в систему координат вершиной A в точку √3/2, ребром ВС по оси Оу.
Координаты точек:
C(0; 1,5; 0), S(√3/2; 1; 3√2), F(√3; 0,5; 02).
По трём точкам находим уравнение плоскости ASC:
ASC: 5,19615x + 9y + 0z - 13,5 = 0 .
Точки A(√3/2; 0; 0), M(√3/2; 1; 3√2).
Вектор MA: (0; 1,5; 3√2/2).
Направляющий вектор прямой имеет вид: l m n
Скалярное произведение 13,5
s = {l; m; n} 0 1,5 2,12132
Модуль = √6,75 = 2,598.
Вектор нормали плоскости имеет вид:
A B C sin fi = 0,5
Ax + By + Cz + D = 0 5,196152423 9 0
Модуль 10,3923.
fi = 0,5236 радиан = 30 градус .
Так как каждый пункт рассматривается в качестве отдельной задачи, замечательные точки треугольника всегда будут называться O.
а) BM₂ точкой пересечения медиан делится в отношении BO : OM₂ = 2 : 1 ⇒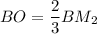 .
.
Так как AB = BC, BM₂ — высота. По теореме Пифагора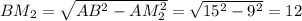 .
.
Тогда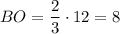
б) Точка пересечения биссектрис — центр вписанной окружности. Так как AB = BC, BB₂ — высота ⇒ OB₂ — радиус (r) вписанной окружности.
Площадь треугольника ABC
в) Точка пересечения серединных перпендикуляров — центр описанной окружности ⇒ OB — радиус (R) описанной окружности. Площадь треугольника ABC
г) Площадь треугольника ABC
ответ: а) 8; б) 7,5; в) 9,375; г) 5,25