в данном случае а = 3, b = 81, c = 10
в данном случае а = 3, b = 3, c = 4
в данном случае а = 3
в данном случае а = 3, b = 4, c = 16
в данном случае а = 3, b = , с =
в данном случае а = 3, b = 3, c = -2
в данном случае c = 2, a = 7, b = 27
в данном случае c = 2, a = 7, b = 21
в данном случае а = 7, b = 27², c = 81
в данном случае а = 7, b = 3², c = 21²
в данном случае а = 7, b = 7, c = -2
в данном случае а = 7
в данном случае а = 3, b = 81, c = 10
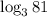
2) Представим 81 как 3⁴в данном случае а = 3, b = 3, c = 4
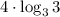
4) Заменим логарифмв данном случае а = 3
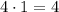
ОТВЕТ 42.в данном случае а = 3, b = 4, c = 16
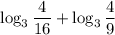
2) По формулев данном случае а = 3, b =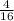 , с =
, с = 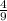
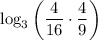
3) Посчитаемв данном случае а = 3, b = 3, c = -2
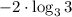
6) Заменим логарифмв данном случае а = 3
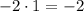
ОТВЕТ -23.в данном случае c = 2, a = 7, b = 27
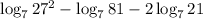
2) Занесем множитель как степеньв данном случае c = 2, a = 7, b = 21
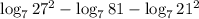
3) По формулев данном случае а = 7, b = 27², c = 81
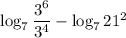
5) Сократим дробьв данном случае а = 7, b = 3², c = 21²
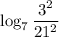
7) Сократим дробь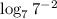
9) Вынесем степень как множительв данном случае а = 7, b = 7, c = -2
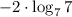
10) Заменим логарифмв данном случае а = 7
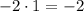
ОТВЕТ -2