Пусть всего детей было n, и у родителей по одному ребенку.
Событие A="Хотя бы один ребенок получит подарок от своих родителей" противоположно событию B="Ни один ребенок не получит подарок от своих родителей". Значит, искомая вероятность .
Найдем количество вариантов раздачи подарков, при которых каждый ребенок получит подарок от чужих родителей.
Рассмотрим таблицу (см. приложение). Столбец соответствует родителям, строка - детям, выбор ячейки на пересечении i-ой строки и j-ого столбца означает, что i-ый ребенок получил подарок от j-ых родителей [ячейки диагонали не рассматриваются, т.к. получение подарка от своих же родителей - неподходящая ситуация]. Требуется выбрать n ячеек такой таблицы так, чтобы в каждом столбце и строке была выбрана ровно одна ячейка [каждый ребенок получил подарок не от своих родителей, и каждый родитель вручил подарок не своему ребенку].
А это известная задача о расстановке ладей, не бьющих друг друга и не находящихся на одной из диагоналей, для которой было получено явное выражение числа вариантов [подробнее, например, Окунев Л. Я. Комбинаторные задачи на шахматной доске. — 1935 , с .8-14]
Пошаговое объяснение:
Пусть всего детей было n, и у родителей по одному ребенку.
Событие A="Хотя бы один ребенок получит подарок от своих родителей" противоположно событию B="Ни один ребенок не получит подарок от своих родителей". Значит, искомая вероятность
.
Найдем количество вариантов раздачи подарков, при которых каждый ребенок получит подарок от чужих родителей.
Рассмотрим таблицу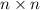
(см. приложение). Столбец соответствует родителям, строка - детям, выбор ячейки на пересечении i-ой строки и j-ого столбца означает, что i-ый ребенок получил подарок от j-ых родителей [ячейки диагонали не рассматриваются, т.к. получение подарка от своих же родителей - неподходящая ситуация]. Требуется выбрать n ячеек такой таблицы так, чтобы в каждом столбце и строке была выбрана ровно одна ячейка [каждый ребенок получил подарок не от своих родителей, и каждый родитель вручил подарок не своему ребенку].
А это известная задача о расстановке ладей, не бьющих друг друга и не находящихся на одной из диагоналей, для которой было получено явное выражение числа вариантов [подробнее, например, Окунев Л. Я. Комбинаторные задачи на шахматной доске. — 1935 , с .8-14]
Всего вариантов раздачи подарков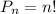
.
Но тогда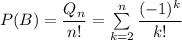
.
Отсюда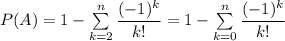
________________________
Теперь рассмотрим ситуацию при
Используя разложение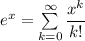
, получим при 
равенство
Значит,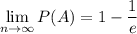
задание 1
Дано число 14. Укажи, какое оно.
ответ: чётное
задание 2
Верно ли, что:
число 64 — кратное числа 8?
ответ: да
задание 3
В каждой коробке лежат 8 фломастеров.
Определи, возможно ли взять несколько коробок, чтобы фломастеров в них лежало ровно 32 шт.
ответ: да
.
задание 4
В одном ящике было 22 кассет(-ы), а в другом — 25.
Можно ли эти кассеты разложить в коробки так, чтобы в каждой было по 5 кассет?
ответ: разделить так
а) нельзя
задание 5
В одном букете было 16 роз, а в другом — 49.
Можно ли эти розы поставить в 6 ваз так, чтобы в каждой вазе цветов было поровну?
ответ: разделить поровну
а) нельзя
задание 6
Укажите ВСЕ делители числа 24.
(может быть два или три ответа)
3, 8, 12, 1, 24, 4, 6
задание 7
В ларьке продаются воздушные шары по цене 2 руб., 5 руб. и 12 руб. Роман хочет купить одинаковые воздушные шары на 90 руб. без сдачи.
Какие воздушные шары Роман может купить шары с этими условиями?
Определи, сколько таких шаров можно купить.
ответ (цену шаров записывай, начиная с наименьшей):
Роман может купить 45шт. шаров по 2руб.
или
Роман может купить 18шт. шаров по 5руб.
задание 8
Выберите все истинные высказывания.
1 является делителем любого натурального числа
12 делится нацело на 3
72 кратно 6
Любое натуральное число кратно самому себе
2 является делителем 16