Вынесем из всех строчек, кроме первой, множитель x, после чего прибавим к первой строчке вторую, умноженную на (в результате в первой строчке на первом месте появится ноль, а на втором месте будет стоять после чего к первой строчке прибавим третью, умноженную на четвертую, умноженную на и так далее, последнюю, умноженную на Получаем
Остается разложить получившийся определитель по первой строчке, после чего получается нижнетреугольная матрица, равная произведению диагональных элементов (а на диагонали стоят единицы).
В результате получается такой ответ:
Конечно, в показателе вместо n+2 можно написать n.
Чтобы в четвертой коробке были два белых шара и один черный, необходимо выбрать из одной из 3 коробок чёрный шар а из двух - белые
Так как внимание шаров из коробок - независимые события, то совместная вероятность равна произведению вероятности
Пусть с первой коробки вытягивает чёрный шар, а со второй и третьей- белые
Р=1/3×1/3×1/3=1/27, так как вероятности вытащить один из трех шаров одинаковые, то вероятность вытащить чёрный шар с первой, второй или третьей коробки - равны
Р(четвертой коробке- два белых шара и один черный)=1/27+1/27+1/27=3/27=1/9
Вынесем из всех строчек, кроме первой, множитель x, после чего прибавим к первой строчке вторую, умноженную на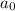 (в результате в первой строчке на первом месте появится ноль, а на втором месте будет стоять
(в результате в первой строчке на первом месте появится ноль, а на втором месте будет стоять 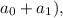 после чего к первой строчке прибавим третью, умноженную на
после чего к первой строчке прибавим третью, умноженную на 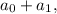 четвертую, умноженную на
четвертую, умноженную на 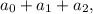 и так далее, последнюю, умноженную на
и так далее, последнюю, умноженную на 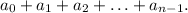 Получаем
Получаем
Остается разложить получившийся определитель по первой строчке, после чего получается нижнетреугольная матрица, равная произведению диагональных элементов (а на диагонали стоят единицы).
В результате получается такой ответ:
Конечно, в показателе вместо n+2 можно написать n.
Відповідь:
Покрокове пояснення:
Вероятность выбрать один из шаров коробки =1/3
Чтобы в четвертой коробке были два белых шара и один черный, необходимо выбрать из одной из 3 коробок чёрный шар а из двух - белые
Так как внимание шаров из коробок - независимые события, то совместная вероятность равна произведению вероятности
Пусть с первой коробки вытягивает чёрный шар, а со второй и третьей- белые
Р=1/3×1/3×1/3=1/27, так как вероятности вытащить один из трех шаров одинаковые, то вероятность вытащить чёрный шар с первой, второй или третьей коробки - равны
Р(четвертой коробке- два белых шара и один черный)=1/27+1/27+1/27=3/27=1/9