Построить график функции и написать все элементарные преобразования этой функции:

К решению прилагается рисунок

Дано: AF, AE - наклонные

AH - перпендикуляр к плоскости α

EH,FH - проекции

∠AFH = 60°

∠AEH = 30°

HE = 6 см

Найти: FH - ?

Решение: 1) Рассмотрим ΔAEH

ΔAEH - прямоугольный, т.к. AH - перпендикуляр к плоскости α

Т.к. ∠AEH = 30° ⇒ AE = 2AH

Пусть x - AH, тогда 2x - AE

По теореме Пифагора

x² + 6² = (2x)²

x² + 36 = 4x²

4x² - x² = 36

3x² = 36

x² = 12

x = √12

2)Рассмотрим ΔAFH

ΔAEH - прямоугольный, т.к. AH - перпендикуляр к плоскости α

Т.к. ∠AFH = 60° ⇒ ∠FAH = 30° ⇒ FH = 2AF

Пусть y - FH, тогда 2y - AF

По теореме Пифагора

y² + (√12)² = (2y)²

y² + 12 = 4y²

4y² - y² = 12

3y² = 12

y² = 4

y = 2

ответ: FH = 2

С первым числом все понятно: оно заканчивается цифрой 5, поскольку любое число, заканчивающееся пятеркой, в любой степени тоже будет заканчиваться цифрой 5.

Со вторым - аналогично: любое число, заканчивающееся шестеркой, в любой степени тоже будет заканчиваться цифрой 6.

С третьим - немного сложнее. Посмотрим, какой цифрой могут заканчиваться степени числа 2017:

и т.д.. Т.е. последнии цифры степеней числа 2017 чередуются в таком порядке - 7, 9, 3, 1 - и повторяются с интервалом в 4 цифры.

Поскольку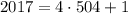 , то последняя цифра числа 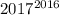- единица. Тогда последняя цифра числа 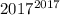- семерка.

Ну а если первое число заканчивается 5, второе - 6, третье - 7, то выражение заканчивается последней цифрой суммы последних цифр всех трех степеней: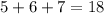 - значит, значение выражения заканчивается цифрой 8.