3) Найдем точки пересечения графика функции с осями координат:
Если , то , значит — точка пересечения с осью .
Если , то есть , то:
Значит , и — точки пересечения с осью .
4) Асимптот данная функция не имеет, поскольку она непрерывная на всей области определения.
5) Найдем производную и критические (стационарные) точки функции:
Из уравнения имеем критические точки:
6) Найдем промежутки возрастания, убывания и экстремумы функции, заполнив таблицу (см. вложение).
7) Исследуем функцию на выпуклость и точки перегиба с второй производной:
Если на промежутке дифференцируемая функция имеет положительную вторую производную, то есть для всех , то график этой функции на является выпуклым вниз; если на промежутке дифференцируемая функция имеет отрицательную вторую производную, то есть для всех , то график этой функции на является выпуклым вверх.
Решим уравнение:
Имеем корни:
Систематизируем данные, полученные по второй производной, в таблице (см. вложение)
8) Изобразим график заданной функции (см. вложение).
9) Из графика можем найти область значений функции:
График прямой задается формулой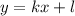 , где
, где 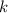 и
и 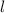 — некоторые коэффициенты,
— некоторые коэффициенты,  — независимая переменная, которая называется линейной функцией.
— независимая переменная, которая называется линейной функцией.
Имеем три точки: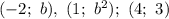 , где
, где 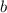 — параметр, который нужно найти.
— параметр, который нужно найти.
Подставляя соответствующие координаты в функцию, получаем систему из трех линейных уравнений с тремя неизвестными:
Из третьего уравнения: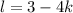 . Подставим
. Подставим 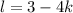 в первое и во второе уравнение:
в первое и во второе уравнение:
Выразим из второго уравнения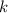 :
:
Подставим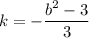 в первое уравнение:
в первое уравнение:
Решим полученное квадратное уравнение через дискриминант:
Таким образом, имеем: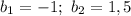
ответ: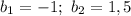
Задана функция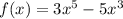
1) Найдем область определения функции:
2) Исследуем функцию на четность:
Функция нечетная, непериодическая.
3) Найдем точки пересечения графика функции с осями координат:
Если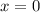 , то
, то 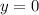 , значит
, значит 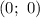 — точка пересечения с осью
— точка пересечения с осью 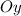 .
.
Если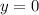 , то есть
, то есть 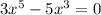 , то:
, то:
Значит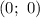 ,
, 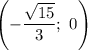 и
и 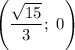 — точки пересечения с осью
— точки пересечения с осью 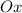 .
.
4) Асимптот данная функция не имеет, поскольку она непрерывная на всей области определения.
5) Найдем производную и критические (стационарные) точки функции:
Из уравнения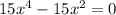 имеем критические точки:
имеем критические точки:
6) Найдем промежутки возрастания, убывания и экстремумы функции, заполнив таблицу (см. вложение).
7) Исследуем функцию на выпуклость и точки перегиба с второй производной:
Если на промежутке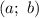 дифференцируемая функция
дифференцируемая функция 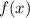 имеет положительную вторую производную, то есть
имеет положительную вторую производную, то есть 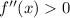 для всех
для всех 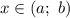 , то график этой функции на
, то график этой функции на 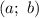 является выпуклым вниз; если на промежутке
является выпуклым вниз; если на промежутке 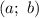 дифференцируемая функция
дифференцируемая функция 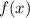 имеет отрицательную вторую производную, то есть
имеет отрицательную вторую производную, то есть 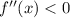 для всех
для всех 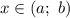 , то график этой функции на
, то график этой функции на 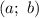 является выпуклым вверх.
является выпуклым вверх.
Решим уравнение: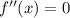
Имеем корни: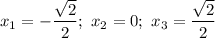
Систематизируем данные, полученные по второй производной, в таблице (см. вложение)
8) Изобразим график заданной функции (см. вложение).
9) Из графика можем найти область значений функции: