Основанием пирамиды является прямоугольный треугольник с катетами, равными 6 и 8 см. каждый из двугранных углов, образованных боковыми гранями и основанием пирамиды, равен 60° найти площадь боковой поверхности пирамиды.
Проведем DO — высоту пирамиды и перпендикуляры DK, DM и DN к соответствующим сторонам ΔАВС.
по теореме о трех перпендикулярах OK ⊥ ВС, ОМ ⊥ АС и ON ⊥ AB. Где ∠DKO = ∠DMO = ∠DNO = 60° — линейные углы данных двугранных углов.
следовательно, треугольники DKO, DMO и DNO равны по катету и острому углу. Тогда OM = OK = ON, то есть точка О является центром окружности, вписанной в основание.
по теореме пифагора в прямоугольном ΔAВС:
найдем площадь ΔAВС
S=1/2*АС*АВ=1/2*6*8=24 кв см
с другой стороны S=pr=24/112= 2 см
тогда ΔDMO
DO=MO*tg60=r Нашли высоту пирамиды
Теперь надо по теореме пифагора найти высоты боковых граней в ΔDКO
надо провести высоту пирамиды.
Проведем DO — высоту пирамиды и перпендикуляры DK, DM и DN к соответствующим сторонам ΔАВС.
по теореме о трех перпендикулярах OK ⊥ ВС, ОМ ⊥ АС и ON ⊥ AB. Где ∠DKO = ∠DMO = ∠DNO = 60° — линейные углы данных двугранных углов.
следовательно, треугольники DKO, DMO и DNO равны по катету и острому углу. Тогда OM = OK = ON, то есть точка О является центром окружности, вписанной в основание.
по теореме пифагора в прямоугольном ΔAВС:
найдем площадь ΔAВС
S=1/2*АС*АВ=1/2*6*8=24 кв см
с другой стороны S=pr=24/112= 2 см
тогда ΔDMO
DO=MO*tg60=r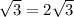 Нашли высоту пирамиды
Нашли высоту пирамиды
Теперь надо по теореме пифагора найти высоты боковых граней в ΔDКO
DO^2+OK^2=DK^2
Sобщ= Sabc+Sabd+Sacd+Sbcd=24+1/2*6*4+1/2*8*4+1/2*10*4=
=24+12+16+20=72 кв см
если только боковая, то
Sбок =Sabd+Sacd+Sbcd=1/2*6*4+1/2*8*4+1/2*10*4=
=12+16+20=48 кв см