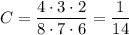Среди выбранных 5 телевизоров с дефектами могут оказаться 0,1,2,3,4 или 5 телевизоров. Таким образом, случайная величина X - количество телевизоров с дефектами среди выбранных - может принимать значения 0,1,2,3,4,5. Найдём соответствующие вероятности:
Всего вариантов последовательно выбрать три карточки: 8 * 7 * 6 (вытянули одну из восьми — осталось семь — затем осталось шесть).
A) Карточка с цифрой 1 может быть вытянута первой, второй или третьей. Тогда в каждом случае осталось семь карточек, а затем шесть: 1 * 7 * 6 + 7 * 1 * 6 + 7 * 6 * 1 = 3 * 7 * 6. Вероятность
B) Чётная карточка может быть вытянута первой, второй или третьей, чётных цифр всего 4 (2, 4, 6, 8). Значит, существует четыре варианта вытянуть чётную карточку, затем остаётся четыре нечётных, затем — три нечётных. То есть подходящих вариантов 4 * 4 * 3 + 4 * 4 * 3 + 4 * 3 * 4 = 4 * 4 * 3 * 3. Вероятность
С) Сначала вытянули одну из четырёх нужных карточек, затем — одну из оставшихся трёх, затем — одну из оставшихся двух. Нужных вариантов: 4 * 3 * 2. Вероятность
Пошаговое объяснение:
Среди выбранных 5 телевизоров с дефектами могут оказаться 0,1,2,3,4 или 5 телевизоров. Таким образом, случайная величина X - количество телевизоров с дефектами среди выбранных - может принимать значения 0,1,2,3,4,5. Найдём соответствующие вероятности:
p0=13/20*12/19*11/18*10/17*9/16=429/5168=1287/15504;
p1=C(7,1)*C(13,4)/C(20,5)=5005/15504 (здесь C(n,k) - число сочетаний из n по k);
p2=C(7,2)*C(13,3)/C(20,5)=6006/15504;
p3=C(7,3)*C(13,2)/C(20,5)=2730/15504;
p4=C(7,4)*C(13,1)/C(20,5)=455/15504;
p5=7/20*6/19*5/18*4/17*3/16=21/15504.
Проверка: p0+p1+p2+p3+p4+p5=15504/15504=1 - значит, вероятности найдены верно.
Составляем ряд распределения случайной величины X:
xi 0 1 2 3 4 5
pi 1287/15504 5005/15504 6006/15504 2730/15504 455/15504 21/15504
Матем. ожидание M[X]=∑xi*pi=7/4; дисперсия D[X]=∑{xi-M[x]}²*pi=273/304.
Пошаговое объяснение:
Всего вариантов последовательно выбрать три карточки: 8 * 7 * 6 (вытянули одну из восьми — осталось семь — затем осталось шесть).
A) Карточка с цифрой 1 может быть вытянута первой, второй или третьей. Тогда в каждом случае осталось семь карточек, а затем шесть: 1 * 7 * 6 + 7 * 1 * 6 + 7 * 6 * 1 = 3 * 7 * 6. Вероятность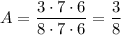
B) Чётная карточка может быть вытянута первой, второй или третьей, чётных цифр всего 4 (2, 4, 6, 8). Значит, существует четыре варианта вытянуть чётную карточку, затем остаётся четыре нечётных, затем — три нечётных. То есть подходящих вариантов 4 * 4 * 3 + 4 * 4 * 3 + 4 * 3 * 4 = 4 * 4 * 3 * 3. Вероятность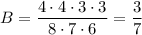
С) Сначала вытянули одну из четырёх нужных карточек, затем — одну из оставшихся трёх, затем — одну из оставшихся двух. Нужных вариантов: 4 * 3 * 2. Вероятность