Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение . Таким образом, синус от 60 градусов равен .
По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
sin (60°) = sin (π/3) = (√3)/2.
Пошаговое объяснение:
Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение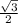 . Таким образом, синус от 60 градусов равен
. Таким образом, синус от 60 градусов равен 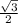 .
.
По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
просто посмотреть значение в таблице.
Пошаговое объяснение:
аₙ=а₁+(n-1)d
а₁ - первый член последовательности
аₙ - член занимающий место n ( 1,2,...n.)
n - номер члена
d - разность между членами ("добавка" которую прибавляют к каждому,чтобы получить последующий)
а₁=2 d=3 2, 2+3, 2+3*2,2+3*3,2+3*4 2 , 5 , 8 , 11 , 14
а₁=0,2 d=0,3 0,2 ; 0,2+0,3 ; 0,2+0,3*2 ; 0,2+0,3*3 ; 0,2+0,3*4
0,2 ; 0,5 ; 0,8 ; 1,1 ; 1,4
а₁= - 0,2 d=0,3 - 0,2 ; -0,2+0,3 ; -0,2+0,3*2 ; -0,2+0,3*3 ; -0,2+0,3*4
- 0,2 ; 0,1 ; 0,4 ; 0,7 ; 1
а₁= 1/2=3/6, d=1/3=2/6 (так легче считать)
3/6 ; 3/6+2/6=5/6 ; 3/6+2/6*2=7/6 ;3/6+2/6 *3=9/6 ;3/6+2/6 *4=11/6
1/2 ; 5/6 ; 1 1/6 ; 1 1/2 ;1 5/6;
а₁= -1/2=3/6, d=-1/3=-2/6 (так легче считать)
-3/6; -3/6-2/6=-5/6; -3/6-2/6*2=-7/6=-1 1/6;-3/6-2/6 *3=-9/6=-1 1/2;
-3/6-2/6 *4=-11/6=-1 5/6
-1/2 ; -5/6 ; -1 1/6 ;- 1 1/2 ; -1 5/6;
а₁= -1/2=3/6, d=1/3=2/6 (так легче считать)
-3/6 ; -3/6+2/6=-1/6 ; -3/6+2/6*2=1/6 ;-3/6+2/6 *3=3/6 ;-3/6+2/6 *4=5/6
-1/2 ; -1/6 ; 1/6 ; 1/2 ; 5/6;