Одиннадцатиклассник Виктор твёрдо решил поступить на математический факультет любимого вуза. Виктор пообещал себе, что даже если не сдаст ЕГЭ на необх. одимый , то и дальше каждый год будет сдавать экзамен до тех пор, пока не сможет поступить. Виктор прекрасно понимает, что шанс поступить сразу после окончания школы равен 0,7, а в каждый последующий год вероятность успешного поступления будет равна 0,4. Какое наименьшее число попыток сдачи экзаменов потребуется для того, чтобы вероятность поступления в любимый вуз была не менее 99%?
8
Пошаговое объяснение:
Найдём вероятность того, что Виктор не поступит после n > 1 попыток.
Вероятность того, что первая попытка сразу после школы будет неудачной, равна 1 - 0,7 = 0,3, а вероятность неуспешной сдачи каждого экзамена после этого 1 - 0,4 = 0,6.
Тогда вероятность того, что Виктор не поступит после n попыток, равна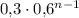 , а вероятность того, что он поступит, соответственно,
, а вероятность того, что он поступит, соответственно, 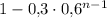 .
.
Вероятность поступления должна быть не менее 0,99, так что
Если верить калькулятору, логарифм в правой части неравенства равен 7,65...., так что наименьшее подходящее n = 8.
Без калькулятора можно построить таблицу значений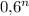 :
:
Несколько минут мучений, и получаем, что первое n, при котором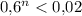 - это n = 8.
- это n = 8.